题目内容
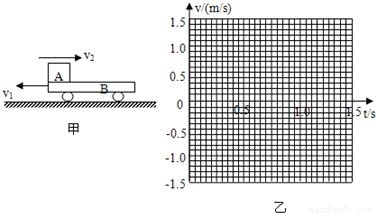
如图甲所示,质量mB=1kg的平板小车B在光滑水平面上以v1=1m/s的速度向左匀速运动.当t=0时,质量mA=2kg的小铁块A以v2=2m/s的速度水平向右滑上小车,A与小车间的动摩擦因数为μ=0.2.若A最终没有滑出小车,取水平向右为正方向,g=10m/s2,求:(1)A在小车上停止运动时,小车的速度为多大?
(2)小车的长度至少为多少?
(3)在图乙所示的坐标纸中画出1.5s内小车B运动的速度一时间图象.
【答案】分析:(1)根据动量守恒定律列式求解即可;
(2)滑块和小车系统减小的动能转化为内能,系统摩擦产生的热量等于滑动摩擦力与相对路程的乘积;根据功能关系列式即可;
(3)先求解匀变速运动时间,最后阶段与小车一起匀速运动.
解答:解:(1)A在小车上停止运动时,A、B以共同速度运动,设其速度为v,取水平向右为正方向,由动量守恒定律得:
mAv2-mBv1=(mA+mB)v
解得,v=lm/s
(2)设小车的最小长度为L,由功能关系得: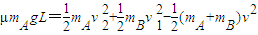
解得:L=0.75m
(3)设小车做变速运动的时间为t,由动量定理得:μmAgt=mB(v+v1)
解得:t=0.5s
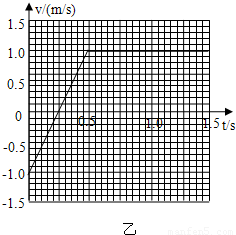
故小车的速度-时间图象如图所示.
答:(1)A在小车上停止运动时,小车的速度为1m/s;
(2)小车的长度至少为0.75m;
(3)如图所示.
点评:本题关键明确小车和滑块的运动规律,然后根据动能定理、动量守恒定律、动量定理等列式后联立求解.
(2)滑块和小车系统减小的动能转化为内能,系统摩擦产生的热量等于滑动摩擦力与相对路程的乘积;根据功能关系列式即可;
(3)先求解匀变速运动时间,最后阶段与小车一起匀速运动.
解答:解:(1)A在小车上停止运动时,A、B以共同速度运动,设其速度为v,取水平向右为正方向,由动量守恒定律得:
mAv2-mBv1=(mA+mB)v
解得,v=lm/s
(2)设小车的最小长度为L,由功能关系得:
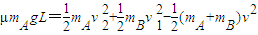
解得:L=0.75m
(3)设小车做变速运动的时间为t,由动量定理得:μmAgt=mB(v+v1)
解得:t=0.5s
故小车的速度-时间图象如图所示.

答:(1)A在小车上停止运动时,小车的速度为1m/s;
(2)小车的长度至少为0.75m;
(3)如图所示.
点评:本题关键明确小车和滑块的运动规律,然后根据动能定理、动量守恒定律、动量定理等列式后联立求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
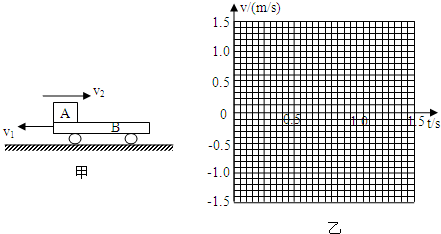



 (3) 如图甲所示,质量mB=1kg的平板小车B在光滑水平面上以v1=1m/s的速度向左匀速运动.当t=0时,质量mA=2kg的小铁块A以v2=2 m/s的速度水平向右滑上小车,A与小车间的动摩擦因数为μ=0.2。若A最终没有滑出小车,取水平向右为正方向,g=10m/s2,求:
(3) 如图甲所示,质量mB=1kg的平板小车B在光滑水平面上以v1=1m/s的速度向左匀速运动.当t=0时,质量mA=2kg的小铁块A以v2=2 m/s的速度水平向右滑上小车,A与小车间的动摩擦因数为μ=0.2。若A最终没有滑出小车,取水平向右为正方向,g=10m/s2,求: