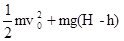题目内容
 如图所示,水平桌面上放置一个质量m=1kg的小木块,若用木棒击打木块使木块获得水平方向的初速度v0,木块沿桌面滑出左端边沿,落在水平地面上的D点.已知木块的初速度v0=20m/s,桌面距地面的高度H=3.2m,木块落地的位置距桌面左端边沿的水平距离x=4.8m,忽略空气阻力,取重力加速度g=10m/s2.求:
如图所示,水平桌面上放置一个质量m=1kg的小木块,若用木棒击打木块使木块获得水平方向的初速度v0,木块沿桌面滑出左端边沿,落在水平地面上的D点.已知木块的初速度v0=20m/s,桌面距地面的高度H=3.2m,木块落地的位置距桌面左端边沿的水平距离x=4.8m,忽略空气阻力,取重力加速度g=10m/s2.求:(1)木块落到地面时的速度大小;
(2)木块离开桌面时的动能;
(3)木块在桌面上滑行过程中克服摩擦力所做的功.
分析:(1)木块离开桌面后做平抛运动,根据平抛运动的规律求解.
(2)木块落地时速度分解成竖直方向和水平方向速度,根据几何关系求解.
(3)根据动能定理求解木块在桌面上滑行过程中克服摩擦力所做的功.
(2)木块落地时速度分解成竖直方向和水平方向速度,根据几何关系求解.
(3)根据动能定理求解木块在桌面上滑行过程中克服摩擦力所做的功.
解答:解:(1)木块离开桌面后做平抛运动,设运动时间为t,根据自由落体公式H=
gt2
木块做平抛运动的时间 t=
=0.8s
木块落地时沿水平方向的分速度 vx=
=6.0 m/s
木块落地时沿竖直方向的分速度 vy=gt=8.0 m/s
木块落到地面时的速度大小 v=
=10.0 m/s
(2)根据动能公式,得木块离开桌面时的动能Ek=
m
=18 J
(3)根据动能定理
W=△Ek=
m
-
m
=-182 J
故木块在桌面上滑行过程中克服摩擦力所做的功为182 J
答:(1)木块落到地面时的速度大小为10.0m/s;
(2)木块离开桌面时的动能18J;
(3)木块在桌面上滑行过程中克服摩擦力所做的功为182J.
| 1 |
| 2 |
木块做平抛运动的时间 t=
|
木块落地时沿水平方向的分速度 vx=
| x |
| t |
木块落地时沿竖直方向的分速度 vy=gt=8.0 m/s
木块落到地面时的速度大小 v=
|
(2)根据动能公式,得木块离开桌面时的动能Ek=
| 1 |
| 2 |
| v | 2 x |
(3)根据动能定理
W=△Ek=
| 1 |
| 2 |
| v | 2 x |
| 1 |
| 2 |
| v | 2 0 |
故木块在桌面上滑行过程中克服摩擦力所做的功为182 J
答:(1)木块落到地面时的速度大小为10.0m/s;
(2)木块离开桌面时的动能18J;
(3)木块在桌面上滑行过程中克服摩擦力所做的功为182J.
点评:分析清楚木块在每个过程的运动状态,根据物体的运动的过程来逐个求解,本题中用到了平抛运动和动能定理,涉及的知识点较多,要求学生要熟练的应用每一部分的知识.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
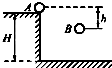 如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )A、
| ||||
B、
| ||||
| C、mgH-mgh | ||||
D、
|
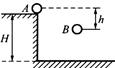
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能的表达式正确的是( ) 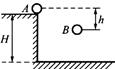
A. | B. |
| C.mgH-mgh | D. |


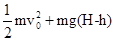

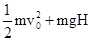 B.
B.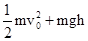


 B.
B.