题目内容
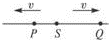 如图所示,波源S从平衡位置y=0开始振动,振动方向为竖直向上(y轴的正方向),振动周期为T=0.01s,产生的简谐波向左、右两个方向传播,波速均为v=80m/s.经过一段时间后,P、Q两点开始振动.已知距离SP=1.2m,SQ=2.6m.若以Q点开始振动时刻作为计时的零点,则在下列振动图象中,能正确描述P、Q两点振动情况的是:( )
如图所示,波源S从平衡位置y=0开始振动,振动方向为竖直向上(y轴的正方向),振动周期为T=0.01s,产生的简谐波向左、右两个方向传播,波速均为v=80m/s.经过一段时间后,P、Q两点开始振动.已知距离SP=1.2m,SQ=2.6m.若以Q点开始振动时刻作为计时的零点,则在下列振动图象中,能正确描述P、Q两点振动情况的是:( )分析:波源P开始振动方向竖直向上,则介质中各起振方向均沿竖直向上方向.由波速公式求出波长.若以Q点开始振动的时刻作为计时的零点,根据S、Q间的距离与波长的关系,分析此时刻S质点的振动方向及振动情况.
解答: 解:由题,该波的周期T=0.01s,
解:由题,该波的周期T=0.01s,
由波速公式v=
得,波长λ=vT=80×0.01m=0.8m
则SP=1.2m=1.5λ、SQ=2.6m=3
λ.
波源S开始振动方向竖直向上,则介质中各起振方向均沿竖直向上方向.结合波形可知,当Q点开始振动时,Q点向上振动,而P点此时处于波谷,则P、Q两点的振动图象为
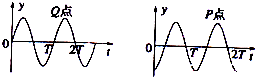
故AD正确,BC错误.
故选:AD.
 解:由题,该波的周期T=0.01s,
解:由题,该波的周期T=0.01s,由波速公式v=
| λ |
| T |
则SP=1.2m=1.5λ、SQ=2.6m=3
| 1 |
| 4 |
波源S开始振动方向竖直向上,则介质中各起振方向均沿竖直向上方向.结合波形可知,当Q点开始振动时,Q点向上振动,而P点此时处于波谷,则P、Q两点的振动图象为
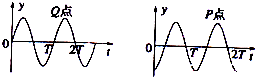
故AD正确,BC错误.
故选:AD.
点评:本题解题时要注意波向右、向左同时传播,两列波的波形左右具有对称性.根据两质点间距离与波长的关系,结合波形,分析两质点间状态和位置关系,是应具有的能力.

练习册系列答案
相关题目

 如图所示,波源S从平衡位置开始上下(y轴方向)振动,产生的简谐波向右传播,经过0.1s后,P点开始振动,已知SP=2m,若以P点开始振动时刻作为计时的起点,图为P点的振动图象,则下列说法正确的是( )
如图所示,波源S从平衡位置开始上下(y轴方向)振动,产生的简谐波向右传播,经过0.1s后,P点开始振动,已知SP=2m,若以P点开始振动时刻作为计时的起点,图为P点的振动图象,则下列说法正确的是( ) 如图所示,波源S从平衡位置开始上、下(沿y轴方向)振动,产生的简谐横波向右传播,经过0.1s后,沿波的传播方向上距S为2m的P点开始振动.若以P点开始振动的时刻作为计时的起点,P点的振动图象,如图所示.则下列说法中正确的是( )
如图所示,波源S从平衡位置开始上、下(沿y轴方向)振动,产生的简谐横波向右传播,经过0.1s后,沿波的传播方向上距S为2m的P点开始振动.若以P点开始振动的时刻作为计时的起点,P点的振动图象,如图所示.则下列说法中正确的是( )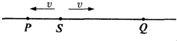 如图所示,波源S从平衡位置y=0开始振动,运动方向竖直向上(y轴的正方向),振动周期T=0.01s,产生的简谐横波向左、右两个方向传播,波速均为v=80m/s.经过一段时间后,P、Q两质元已开始振动.已知距离SP=1.2m,SQ=2.6m,若以Q质元开始振动的时刻作为计时的零点,则P质元的振动图象是( )
如图所示,波源S从平衡位置y=0开始振动,运动方向竖直向上(y轴的正方向),振动周期T=0.01s,产生的简谐横波向左、右两个方向传播,波速均为v=80m/s.经过一段时间后,P、Q两质元已开始振动.已知距离SP=1.2m,SQ=2.6m,若以Q质元开始振动的时刻作为计时的零点,则P质元的振动图象是( )