题目内容
5.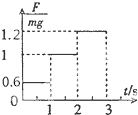 2014年10月7日,云南景谷地震发生后,成都军区第14集团军某旅300名官兵和地震应急救援队200名官兵抵达震中展开地毯式搜索.假设在开展抢险救援过程中,某官兵背起伤员从危楼中沿安全绳由静止开始往地面滑行,经过3s时间安全落地.已知下滑过程中轻绳受到的拉力与伤员和官兵总重力的比值随时间变化的情况加图所示.g=10m/s2,求:
2014年10月7日,云南景谷地震发生后,成都军区第14集团军某旅300名官兵和地震应急救援队200名官兵抵达震中展开地毯式搜索.假设在开展抢险救援过程中,某官兵背起伤员从危楼中沿安全绳由静止开始往地面滑行,经过3s时间安全落地.已知下滑过程中轻绳受到的拉力与伤员和官兵总重力的比值随时间变化的情况加图所示.g=10m/s2,求:(1)伤员与官兵下滑的最大速度;
(2)伤员被救楼层离地面的高度.
分析 (1)根据图象知人先加速后匀速再减速,通过牛顿第二定律求出0-1s加速度,根据v=at求速度为最大速度;
(2)分别求出各段的加速度,根据速度关系,利用运动学公式求的速度和位移.
解答 解:(1)由图可知在t=1s时,速度最大,
由牛顿第二运动定律得mg-F1=ma1
其中在0~1s内F1=0.6mg,
解得:a1=4m/s2,
最大速度vm=a1t1=4×1=4m/s
(2)在第0~1s内选手与伤员运动距离:
x1=$\frac{1}{2}$a1t12=$\frac{1}{2}$×4×12=2m,
在1~2s内官兵与伤员受力平衡,
做匀速直线运动,位移:x2=vmt2=4×1=4m,
在2~3s内由牛顿第二运动定律得:
F2-mg=ma2,其中:F2=1.2mg,解得:a2=2m/s2
在这段时间内下滑的末速度为:vt=vm-a2t3=2m/s
减速下滑距离为x3=$\frac{{v}_{m}+{v}_{t}}{2}$t3=$\frac{4+2}{2}$×1=3m
伤员被救楼层距离地面的高度为:x=x1+x2+x3=9m
答:(1)伤员与官兵下滑的最大速度的大小为4m/s.
(2)伤员被救楼层距离地面的高度为9m.
点评 本题主要考查了求最大速度与楼的高度问题,分析清楚图示图象、判断出伤员与官兵的运动过程与运动性质是解题的关键,应用牛顿第二定律与运动学公式可以解题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
16. 在某水平方向的电场线AB上(电场线方向未标明),将一受到水平向右恒定拉力的带电粒子(不计重力)在A点由静止释放,带电粒子沿AB方向开始运动,经过B点时的速度恰好为零,则下列结论正确的是( )
在某水平方向的电场线AB上(电场线方向未标明),将一受到水平向右恒定拉力的带电粒子(不计重力)在A点由静止释放,带电粒子沿AB方向开始运动,经过B点时的速度恰好为零,则下列结论正确的是( )
 在某水平方向的电场线AB上(电场线方向未标明),将一受到水平向右恒定拉力的带电粒子(不计重力)在A点由静止释放,带电粒子沿AB方向开始运动,经过B点时的速度恰好为零,则下列结论正确的是( )
在某水平方向的电场线AB上(电场线方向未标明),将一受到水平向右恒定拉力的带电粒子(不计重力)在A点由静止释放,带电粒子沿AB方向开始运动,经过B点时的速度恰好为零,则下列结论正确的是( )| A. | 粒子的运动不可能是匀速运动,也不可能是匀加速运动 | |
| B. | 可能A点的电势高于B点的电势,也可能A点的电势低于B点的电势 | |
| C. | A处的场强可能大于B处的场强 | |
| D. | 粒子在A.B两点间移动时,恒力做功的数值大于粒子在A、B两点间的电势能之差的绝对值 |
20.已知分运动求合运动,叫做运动的合成;已知合运动求分运动,叫做运动的分解,关于运动的合成与分解,下列说法正确的是( )
| A. | 合运动的位移等于分运动位移的矢量和 | |
| B. | 合运动的速度等于分运动速度的矢量和 | |
| C. | 合运动的时间等于分运动的时间之和 | |
| D. | 运动的合成与分解遵循平行四边形定则 |
1.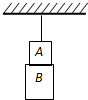 如图所示,用细绳将磁铁A竖直挂起,再将小铁块B吸附在磁铁A的下端,静止后将细线烧断,A、B同时下落,不计空气阻力.则下落过程中( )
如图所示,用细绳将磁铁A竖直挂起,再将小铁块B吸附在磁铁A的下端,静止后将细线烧断,A、B同时下落,不计空气阻力.则下落过程中( )
 如图所示,用细绳将磁铁A竖直挂起,再将小铁块B吸附在磁铁A的下端,静止后将细线烧断,A、B同时下落,不计空气阻力.则下落过程中( )
如图所示,用细绳将磁铁A竖直挂起,再将小铁块B吸附在磁铁A的下端,静止后将细线烧断,A、B同时下落,不计空气阻力.则下落过程中( )| A. | 小铁块B一定受三个力的作用 | |
| B. | 磁铁A向下的加速度大于重力加速度 | |
| C. | 小铁块B的加速度小于重力加速度 | |
| D. | 磁铁A对小铁块B的压力为零 |
 从A处自由释放一个弹性球,与水平地面一次碰撞后等速率竖直反弹,在B处被接住,总的运动时间为2.2s.已知球在被接住前1s内(在反弹后)通过的位移大小为3m,方向竖直向上,不计空气阻力,g取10m/s2,试求A处距离地面的高度.
从A处自由释放一个弹性球,与水平地面一次碰撞后等速率竖直反弹,在B处被接住,总的运动时间为2.2s.已知球在被接住前1s内(在反弹后)通过的位移大小为3m,方向竖直向上,不计空气阻力,g取10m/s2,试求A处距离地面的高度.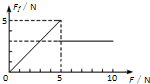 将质量为1.0kg的木块放在水平长木板上,用力沿水平方向拉木块,拉力从0开始逐渐增大,木块先静止后相对木板运动.用力传感器采集木块受到的拉力和摩擦力的大小,并用计算机绘制出摩擦力大小F1随拉力大小F变化的图象,如图所示,木块与长木板间的动摩擦因数为( )
将质量为1.0kg的木块放在水平长木板上,用力沿水平方向拉木块,拉力从0开始逐渐增大,木块先静止后相对木板运动.用力传感器采集木块受到的拉力和摩擦力的大小,并用计算机绘制出摩擦力大小F1随拉力大小F变化的图象,如图所示,木块与长木板间的动摩擦因数为( ) 一质量为2kg的物块置于水平地面上.当用10N的水平拉力F拉物块时,物块做匀速直线运动.如图所示,现将拉力F改为与水平方向成37°角,大小仍为10N,物块开始在水平地面上运动.(sin 37°=0.6,cos 37°=0.8,g取10m/s2) 求:
一质量为2kg的物块置于水平地面上.当用10N的水平拉力F拉物块时,物块做匀速直线运动.如图所示,现将拉力F改为与水平方向成37°角,大小仍为10N,物块开始在水平地面上运动.(sin 37°=0.6,cos 37°=0.8,g取10m/s2) 求: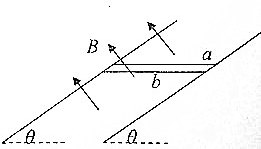 如图所示.两根足够长、电阻不计的平行光滑金属导轨相距L,导轨平面与水平面成θ角,质量均为m、阻值均为R的金属棒a、b紧挨着放在两导轨上,整个装置处于垂直于导轨平面的匀强磁场中,磁场的磁感应强度大小为B.a棒固定,b棒由静止释放,直至b棒刚好匀速时,a、b棒间距离为x,棒与导轨始终垂直并保持良好的接触,重力加速度为g.求:
如图所示.两根足够长、电阻不计的平行光滑金属导轨相距L,导轨平面与水平面成θ角,质量均为m、阻值均为R的金属棒a、b紧挨着放在两导轨上,整个装置处于垂直于导轨平面的匀强磁场中,磁场的磁感应强度大小为B.a棒固定,b棒由静止释放,直至b棒刚好匀速时,a、b棒间距离为x,棒与导轨始终垂直并保持良好的接触,重力加速度为g.求: