题目内容
2.为防止汽车相撞,需要检测汽车的制动性能,并使两辆汽车相距一定的距离,假设汽车的刹车过程是匀减速运动.下面我们作出几种假设.请利用运动学知识计算,在各种情况下,两车至少要相距多远才能避免相撞.假设1:甲、乙两车以相等的速率v在同-直线 上相向而行,从某一时刻起,两车同时制动,以同样大小的加速度a故匀减速运动,为避免撞车,开始制动时两车之间的距离至少为多少?
假设2:甲、乙两车以相等的速率v在同一直线上相向而行,从某一时刻起,甲车先制动,以加速度a做减速运动,当甲车停止时,乙车开始制动,以同样的加速度a做减速运动,为避免撞车,甲车开始制动时.两车之间的距离至少为多少?
假设3:假设甲车与乙车同向行驶.甲车以速度v向前行驶,突然发现正前方有一辆乙车以$\frac{v}{2}$的速度匀速行驶,为避免撞车,甲车开始以加速度a制动时,两车之间的距离为多少?
你还能进一步作出其他假设,并用学过的知识进行解答吗?这是个具有散发思维的问题,希望同学们能认真的想一想,培养自己的发散思维能力.
分析 当甲乙两车相向运动,同时制动,结合速度位移公式求出两车的距离,从而得出两车之间的至少距离.
当甲乙两车相向运动,甲车先制动,注意甲车制动的过程中,乙车做匀速直线运动,结合乙车匀速运动的位移,以及两车匀减速运动的位移,求出两车之间的最小距离.
当甲乙两车同向运动,结合速度时间公式求出速度相等经历的时间,根据位移公式,结合位移关系求出两车之间的最小距离.
解答 解:(1)两车相向而行,两车速度减为零的位移${x}_{1}=\frac{{v}^{2}}{2a}$,
则开始制动时两车之间的距离至少为$△x=2{x}_{1}=\frac{{v}^{2}}{a}$.
(2)甲车先制动,制动的时间$t=\frac{v}{a}$,在制动时间内,乙车的位移${x}_{2}=vt=\frac{{v}^{2}}{a}$,
则开始制动前两车知己的距离至少为$△x=2{x}_{1}+{x}_{2}=\frac{{v}^{2}}{a}+\frac{{v}^{2}}{a}=\frac{2{v}^{2}}{a}$.
(3)两车速度相等经历的时间$t′=\frac{v-\frac{v}{2}}{a}=\frac{v}{2a}$,
此时甲车的位移$x′=\frac{{v}^{2}-\frac{{v}^{2}}{4}}{2a}=\frac{3{v}^{2}}{8a}$,乙车的位移$x″=\frac{v}{2}t′=\frac{{v}^{2}}{4a}$,
则两车之间的距离至少为$△x=x′-x″=\frac{{v}^{2}}{8a}$.
答:三种假设两车间的距离至少分别为$\frac{{v}^{2}}{a}$、$\frac{2{v}^{2}}{a}$、$\frac{{v}^{2}}{8a}$.
点评 本题考查了运动学中的追及相遇问题,关键抓住位移关系,结合运动学公式灵活求解,难度中等.

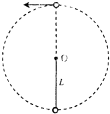 在轨道上稳定运行的空间站中,现有如图所示的装置,轻杆长为L,一端固定在水平轴上的O点,另一端系一个小球(可视为质点).小球以O为圆心在竖直平面内做圆周运动,g为地球表面的重力加速度.下列说法正确的是( )
在轨道上稳定运行的空间站中,现有如图所示的装置,轻杆长为L,一端固定在水平轴上的O点,另一端系一个小球(可视为质点).小球以O为圆心在竖直平面内做圆周运动,g为地球表面的重力加速度.下列说法正确的是( )| A. | 小球通过最高点时速度不可能小于$\sqrt{gL}$ | |
| B. | 小球通过最高点时所受轻杆的作用力可能为零 | |
| C. | 小球通过最高点时所受轻杆的作用力随小球速度的增大而增大 | |
| D. | 小球通过最高点时所受轻杆的作用力大小F2与小球通过最低点时所受轻杆的作用力大小F1一定相等 |
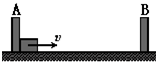 如图,平直路面上有A、B两固定挡板,相距6m,一物块以8m/s的初速度从紧靠A板处出发,摩擦力的作用下在A、B两板间来回做匀减速运动,加速度大小不变.物块每次与A、B板碰撞后以原速率被反弹回去,现要求物块最终停在距B板2m处,已知物块和A挡板只碰撞了一次,则物块的加速度大小可能为( )
如图,平直路面上有A、B两固定挡板,相距6m,一物块以8m/s的初速度从紧靠A板处出发,摩擦力的作用下在A、B两板间来回做匀减速运动,加速度大小不变.物块每次与A、B板碰撞后以原速率被反弹回去,现要求物块最终停在距B板2m处,已知物块和A挡板只碰撞了一次,则物块的加速度大小可能为( )| A. | 1.2 m/s2 | B. | 1.6 m/s2 | C. | 2.0 m/s2 | D. | 2.4 m/s2 |
 如图所示,E为电源,其内阻不可忽略,RT为热敏电阻,阻值随L为指示灯泡,C为平行板电容器,P为理想二极管.闭合开关S,当环境温度明显升高时,下列说法正确的是( )
如图所示,E为电源,其内阻不可忽略,RT为热敏电阻,阻值随L为指示灯泡,C为平行板电容器,P为理想二极管.闭合开关S,当环境温度明显升高时,下列说法正确的是( )| A. | L变暗 | B. | RT两端电压变大 | ||
| C. | C所带的电荷量保持不变 | D. | C所带的电荷量变小 |
| A. | 用同样的力对小车做功,让小车通过的距离依次是 s、2s、3s…进行实验时,力对小车做的功就分别是 W、2W、3W… | |
| B. | 让小车通过相同的距离,所用的力分别为F、2F、3F…进行实验时,力对小车做的功就分别是 W、2W、3W… | |
| C. | 在实验中每次橡皮筋拉伸的长度保持一致,当用 1 条、2 条、3 条…同样的橡皮筋进行实验时,橡皮筋对小车做的功就分别是 W、2W、3W… | |
| D. | 利用弹簧测力计测量对小车的拉力 F 和小车在拉力作用下移动的距离 s,便可以求出每次实验中力对小车做的功,可控制为 W、2W、3W… |
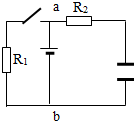 如图所示,电源的电动势E=10V,内阻r=2Ω,电阻R1=8Ω,R2=2Ω,电容器的电容C=20μF.开关原来断开,后将它闭合.求:
如图所示,电源的电动势E=10V,内阻r=2Ω,电阻R1=8Ω,R2=2Ω,电容器的电容C=20μF.开关原来断开,后将它闭合.求: