题目内容
19.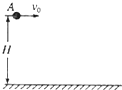 如图所示,在距地面高为H=45m处,有一个小球A以初速度V0=10m/s水平抛出,A可视为质点,空气阻力不计,重力加速度取g=10m/s2,求A球在空中运动时间及其运动的水平距离.
如图所示,在距地面高为H=45m处,有一个小球A以初速度V0=10m/s水平抛出,A可视为质点,空气阻力不计,重力加速度取g=10m/s2,求A球在空中运动时间及其运动的水平距离.
分析 小球做平抛运动,将运动分解成竖直方向的自由落体运动与水平方向的匀速直线运动,根据高度h,由位移公式即可求解时间;根据匀速运动的位移公式,可求出水平距离.
解答 解:小球做平抛运动,竖直方向做自由落体运动,则有
H=$\frac{1}{2}g{t}^{2}$,得 t=$\sqrt{\frac{2H}{g}}$=$\sqrt{\frac{2×45}{10}}$=3s
小球水平方向做匀速直线运动,则水平距离为 x=v0t=30m
答:A球在空中运动时间是3s,其运动的水平距离是30m.
点评 解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,运用运动学公式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.一汽车沿直线运动,开始1/4的时间以16m/s的速度行驶,余下的时间以20m/s的速度行驶,则汽车从开始到行驶完全程这段时间内的平均速度大小为( )
| A. | 18m/s | B. | 19m/s | C. | 19.5m/s | D. | 20m/s |
7. 物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因素分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a与拉力F的关系图线如图所对应的直线甲、乙、丙所示,甲、乙两直线平行,则以下说法正确的是( )
物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因素分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a与拉力F的关系图线如图所对应的直线甲、乙、丙所示,甲、乙两直线平行,则以下说法正确的是( )
 物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因素分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a与拉力F的关系图线如图所对应的直线甲、乙、丙所示,甲、乙两直线平行,则以下说法正确的是( )
物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因素分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a与拉力F的关系图线如图所对应的直线甲、乙、丙所示,甲、乙两直线平行,则以下说法正确的是( )| A. | μA<μB mA=mB | B. | μB>μC mB>mC | ||
| C. | μB=μC mB<mC | D. | μA<μC mA>mC |
14.如果已知万有引力常量G,月球表面的重力加速度g,月球的半径R和月球绕地球运转的周期T,则月球的质量可表示为( )
| A. | $\frac{g{R}^{2}}{G}$ | B. | $\frac{G{R}^{2}}{g}$ | C. | $\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$ | D. | $\frac{{T}^{2}{R}^{3}}{4{π}^{2}G}$ |
11. 一质点沿x轴做直线运动,其v-t图象如图所示,质点在t=0时位于x=3m处,开始沿x轴正向运动( )
一质点沿x轴做直线运动,其v-t图象如图所示,质点在t=0时位于x=3m处,开始沿x轴正向运动( )
 一质点沿x轴做直线运动,其v-t图象如图所示,质点在t=0时位于x=3m处,开始沿x轴正向运动( )
一质点沿x轴做直线运动,其v-t图象如图所示,质点在t=0时位于x=3m处,开始沿x轴正向运动( )| A. | 当t=4s时,质点在x轴上的位置为x=6m | |
| B. | 当t=4s时,质点加速度方向发生变化 | |
| C. | 当t=8s时,质点回到出发点 | |
| D. | 当t=8s时,质点的加速度为1m/s2 |
8.一个物体的加速度为2m/s2,如果作用在物体上的合力增大到原来的两倍,质量减少一半,则物体的加速度将变为( )
| A. | 16m/s2 | B. | 8m/s2 | C. | 4m/s2 | D. | 2m/s2 |
9. 如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是( )
如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是( )
 如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是( )
如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是( )| A. | 轻杆对小球的作用力为2N,方向垂直斜面向上 | |
| B. | 轻杆对小球的作用力为2N,方向竖直向上 | |
| C. | 地面对斜面的支持力小于2N | |
| D. | 地面对斜面的摩擦力水平向右 |
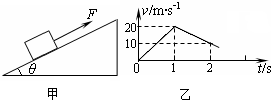 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.试求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.试求: