题目内容
平静的湖面上浮着一只长L="6" m、质量为550 kg的船，船头上站着一质量为m="50" kg的人，开始时，人和船均处于静止.若船行进时阻力很小，问当人从船头走到船尾时，船将行进多远？
0.5 m?
以人和船组成的系统为研究对象.因船行进时阻力很小，船及人所受重力与水对船的浮力平衡，可以认为人在船上行走时系统动量守恒.开始时人和船都静止，系统总动量为零，当人在船上走动时，无论人的速度如何，系统的总动量都保持为零不变.
取人运动方向为正方向，设人对岸的速度为v，船对岸的速度为V，其方向与v相反，由动量守恒定律有0=mv+(-MV)
解得两速度大小之比为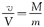
此结果对于人在船上行走过程的任一瞬时都成立.
方法一：取人在船上行走时任一极短时间为Δti，在此时间内人和船都可视为匀速运动，此时间内人和船相对地面移动的距离分别为Δsmi=viΔti和ΔsMi=ViΔti，由此有
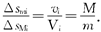
这样人从船头走到船尾时，人和船相对地面移动的总距离分别为
sm=ΣΔsmi，sM=ΣΔsMi.
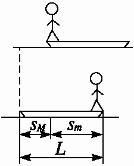
图2
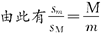
由图2中几何关系可知sm+sM=L.这样，人从船头走到船尾时，船行进的距离为
代入数据有sM="0.5" m.
方法二：由于对于人在船上行走过程的任一时刻都有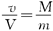
则在该过程中人和船的平均速度应满足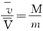
由于人和船运动时间相同，故有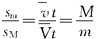
同方法一，可求得sM="0.5" m.
取人运动方向为正方向，设人对岸的速度为v，船对岸的速度为V，其方向与v相反，由动量守恒定律有0=mv+(-MV)
解得两速度大小之比为
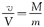
此结果对于人在船上行走过程的任一瞬时都成立.
方法一：取人在船上行走时任一极短时间为Δti，在此时间内人和船都可视为匀速运动，此时间内人和船相对地面移动的距离分别为Δsmi=viΔti和ΔsMi=ViΔti，由此有
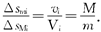
这样人从船头走到船尾时，人和船相对地面移动的总距离分别为
sm=ΣΔsmi，sM=ΣΔsMi.
图2
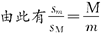
由图2中几何关系可知sm+sM=L.这样，人从船头走到船尾时，船行进的距离为
代入数据有sM="0.5" m.
方法二：由于对于人在船上行走过程的任一时刻都有
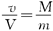
则在该过程中人和船的平均速度应满足
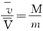
由于人和船运动时间相同，故有
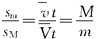
同方法一，可求得sM="0.5" m.
练习册系列答案
相关题目
kg/m3，水在最高点和落至石头上后的速度都认为是零．（落在石头上的水立即流走，在讨论石头对水的作用时可以不考虑水的重力，g取10m/s2） （13分）
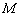的大炮，沿水平方向发射一颗质量为 
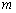的炮弹，在炮身固定不动和可以自由反冲两情况下，炮弹的初速度之比为（ ）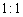
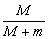
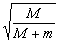
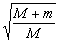
（1）物块与接触面的动摩擦因数μ；