Question

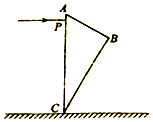
【题目】如图所示，一质量m=4.0kg的小球在轻质弹簧和细线的作用下处于静止状态，细线AO与竖直方向的夹角θ=37°，弹簧BO水平并处于压缩状态，小球与弹簧接触但不粘连，已知弹簧的劲度系数k=100N/m，取sin37°=0.6，cos37°=0.8，求：

（1）小球静止时，细线中的拉力T和弹簧的压缩量x；
（2）剪断细线AB瞬间，小球的加速度a．

Answer 1

【答案】
（1）解：小球的受力图如图，

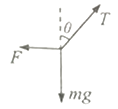
根据平衡条件可知：弹簧的弹力F=mgtanθ

而F=kx

解得：T=50N，x=0.3m

（2）解：剪断细线的瞬间，小球受到重力、弹力不变；合力与原细线中的拉力T等大反向，

则 = 方向与竖直方向成角370，斜向下沿原细线AB方向

【解析】（1）对小球根据受力平衡求出细线中的拉力T和弹簧的弹力，根据胡克定律求出弹簧的压缩量；（2）剪断细线的瞬间弹簧的弹力没有变化，小球受到重力、弹力不变；合力与原细线中的拉力T等大反向，根据牛顿第二定律求出小球的加速度，方向与原来细线的拉力方向相反；