Question

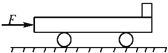
【题目】如图所示，一质量为m的木块，从倾角θ=370的斜面上的A点静止下滑，A与斜面间动摩擦因数μ1=0．25，A到斜面底端B的长度x=2．5m;A通过一段很小的平滑曲面（速度大小不变）到达光滑的平台，紧挨平台且与平台等高的水平传送带，水平段长L=6m，皮带轮轴心固定且顺时针转动，传送带在皮带的带动下以恒定的速度v匀速运动，物块与传送带间的动摩擦因数μ2=0．2，g=10m/s2，（sin370=0．6，cos370=0．8）求：

（1）小物块滑到斜面底端B时的速度大小v1；

（2）若传送带的速度v=0．5m/s，物块滑到水平段最右端C点时的速度vC；

（3）若传送带的速度v/=2m/s，物块滑到水平段最右端C点时的速度v/C；

Answer 1

【答案】（1）5m/s（2）1m/s（3）2m/s

【解析】试题分析：（1）物体由静止沿斜面下滑，由牛顿定律可得：

由运动公式：v12=2a1x

解得v1=5m/s

（2）在传送带上有：

若物体一直减速运动，到达C点时的速度设为v0，由v12-v02=2a2L可得

v0=1m/s

由v0>v可得vC=v0=1m/s

（3）可得