题目内容
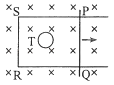
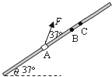
【题目】一台质谱仪的工作原理如图所示．大量的甲、乙两种离子飘入电压力为U0的加速电场，其初速度几乎为0，经过加速后，通过宽为L的狭缝MN沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中，最后打到照相底片上．已知甲、乙两种离子的电荷量均为+q，质量分别为2m和m，图中虚线为经过狭缝左、右边界M、N的甲种离子的运动轨迹．不考虑离子间的相互作用．
（1）求甲种离子打在底片上的位置到N点的最小距离x；
（2）在答题卡的图中用斜线标出磁场中甲种离子经过的区域，并求该区域最窄处的宽度d；
（3）若考虑加速电压有波动，在（U0﹣△U）到（U0+△U）之间变化，要使甲、乙两种离子在底片上没有重叠，求狭缝宽度L满足的条件．
【答案】
（1）
设甲种离子在磁场中的运动半径为r1
电场加速由动能定理得 
再由 
解得 
根据几何关系x=2r1﹣L
解得 
答：甲种离子打在底片上的位置到N点的最小距离x为 
；
（2）
最窄处位于过两虚线交点的垂线上
解得 
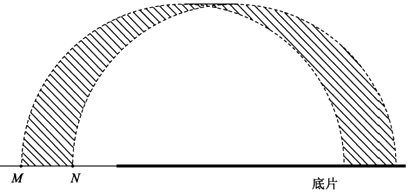
答：在答题卡的图中用斜线标出磁场中甲种离子经过的区域如上图所示，该区域最窄处的宽度d为 
；
（3）
设乙种离子在磁场中的运动半径为 
的最小半径
的最大半径 
由题意知 
，即 
﹣ 
＞L
解得L＜ 
[2 
﹣ 
]
答：若考虑加速电压有波动，在（U0﹣△U）到（U0+△U）之间变化，要使甲、乙两种离子在底片上没有重叠，狭缝宽度L满足的条件
L＜ [2 ﹣ ]
【解析】（1）从M进入磁场的粒子打在底片上的位置到N点距离最小，由动能定理求出粒子进入磁场的速度，根据洛伦兹力提供向心力求出轨道半径，由几何关系即可求解甲种离子打在底片上的位置到N点的最小距离x；
（2）就是将一个虚线半圆平移到另一个虚线半圆，最窄处位于过两虚线交点的垂线上，把两个虚线圆心找到，并连接两圆的最高点，两个圆的最高点的距离为L，根据几何关系求解；
（3）从M点射进磁场的最慢甲种离子即加速电压最小时到底片的距离，比从N点射入得最快的乙种离子即加速电压最大时到达底片的距离要大L，两轨迹的直径相差为L，列式即可求解；
