题目内容
【题目】如图甲所示，y轴右侧空间有垂直xoy平面向里的匀强磁场，同时还有沿-y方向的匀强电场（图中电场未画出）。磁感应强度随时间变化规律如图乙所示（图中B0已知，其余量均为未知）．t=0时刻,一质量为m、电荷量为+q的带电粒子以速度v0从坐标原点O沿x轴射入电场和磁场区，t0时刻粒子到达坐标为（x0,y0）的点A (x0>y0)，速度大小为v，方向沿+x方向，此时撤去电场．t=t0+t1+t2时刻,粒子经过x轴上x=x0点，速度沿+x方向．不计粒子重力，求：
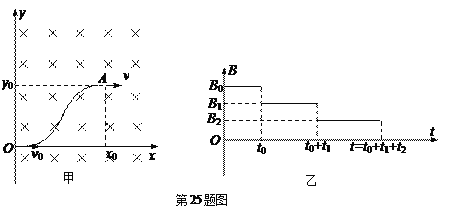
（1）0-t0时间内OA两点间电势差UOA；
（2）粒子在t=0时刻的加速度大小a0；
（3）B1的最小值及对应t2的表达式。
【答案】（1）
（2）
（3）
（k=0，1，2……）
【解析】（1）带电粒子由O到A运动过程中，由动能定理
解得
（2）设电场强度大小为E，则
t=0时刻，由牛顿第二定律
解得
（3）
时间内，粒子在小的虚线圆上运动， 
时刻粒子从C点切入大圆，大圆最大半径为
，相应小圆最大半径为R，则
又
的最小值
对应于
取最小值，带电粒子由C点到经过x轴上
点的时间
满足
（k=0，1，2……）
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
