题目内容
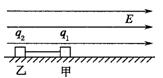
如图所示，在方向水平向右、大小为E＝6×103 N／C的匀强电场中有一个光滑的绝缘平面. 一根绝缘细绳两端分别系有带电滑块甲和乙，甲的质量为m1＝2×10－4 kg，带电量为q1＝2×10－9 C，乙的质量为m2＝1×10－4 kg，带电量为q2＝－1×10－9 C. 开始时细绳处于拉直状态．由静止释放两滑块，t＝3 s时细绳突然断裂，不计滑块间的库仑力，试求∶
（1）细绳断裂前，两滑块的加速度；
（2）在整个运动过程中，乙的电势能增量的最大值；
（3）当乙的电势能增量为零时，甲与乙组成的系统机械能的增量。
（1）绳断前，对甲和乙整体分析有：
（2分）
（1分）
（2）当乙向右运动的速度减为零时，乙的电势能增量最大.
绳断前，乙的位移为：
（1分）
绳断时，乙的速度为：
（1分）
绳断后对乙：
（2分）
乙减速运动的位移： 
（1分）
由功能关系可得，乙的电势能增量为：
（2分）
（3）法一：分析可知，当乙回到出发点时，电场力对其做功为零，其电势能增量为零；
设从绳断至乙回到出发点用时为t1，则有：
代入数据可解得
（2分）
此段时间内，甲加速运动的位移为x3，即
（1分）
（1分）
由功能关系可知，电场力做功使系统机械能增加，故机械能增量为
（2分）
法二：分析可知，当乙回到出发点时，电场力对其做功为零，其电势能增量为零；
设从绳断至乙回到出发点用时为t1，则有：
代入数据可解得
此段时间内，甲加速运动的加速度为a1，即
末态时刻，甲、乙的速度分别为
故系统机械能增量为 
解析:
略
如图所示，在方向水平向右、大小为E=6×103 N/C的匀强电场中有一个光滑的绝缘平面．一根绝缘细绳两端分别系有带电滑块甲和乙，甲的质量为m1=2×10-4 kg，带电量为q1=2×10-9 C，乙的质量为m2=1×10-4 kg，带电量为q2=-1×10-9 C．开始时细绳处于拉直状态．由静止释放两滑块，t=3s时细绳突然断裂，不计滑块间的库仑力，试求：
（2012?昆明模拟）如图所示，在方向水平的匀强电场中，一个不可伸长的不导电轻细线的一端连着一个质量为m的带电小球，另一端固定于O点，把小球拉直至细线与电场方向平行，然后无初速释放，已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ．求小球经过最低点时细线对小球的拉力．
如图所示，在方向水平向右的匀强电场中，一不可伸长的不导电细线的一端连着一个质量为m的带电小球，另一端固定于O点，当小球静止在B点时，细线与竖直方向夹角θ=30°问：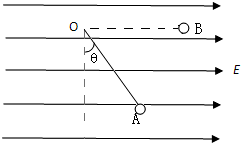
如图所示，在方向水平向右的匀强电场中，一长为L的不可伸长的不导电细线的一端连着一个质量为m的带电量为q小球，另一端固定于O点，小球恰能静止于电场中A点，OA连线与竖直向成θ角且θ=37°．现把小球拉起至细线成水平方向（如图中虚线OB所示），然后无初速释放．（取sin37°=0.6，cos37°=0.8）求：
如图所示，在方向水平向左的匀速电场中有一倾角为60°、高为H的固定绝缘斜面体，现将一质量为m，带正电且电荷量为q的小物块（可视为质点）从斜面体顶端由静止释放，已知重力加速度为g，匀强电场的电场强度大小为E=
| ||
| q |
| A、小物块将沿斜面下滑 | ||
| B、小物块将做曲线运动 | ||
C、小物块到达地面时的速度大小为2
| ||
| D、若其他条件不变，只增大电场强度，小物块到达地面前的运动时间将增大 |