题目内容
（2000?上海）风洞实验室中可产生水平方向的．大小可调节的风力．现将一套有小球的细直杆放入风洞实验室，小球孔径略大于细杆直径．（1）当杆在水平方向上固定时，调节风力的大小，使小球在杆上作匀速运动，这时小球所受的风力为小球所受重力的0.5倍，求小球与杆间的滑动摩擦因数．
（2）保持小球所受风力不变，使杆与水平方向间夹角为37°并固定，则小球从静止出发在细杆上滑下距离S所需时间为多少？（sin37°=0.6，co37°=0.8）
分析：（1）对小球受力分析，受重力、支持力、推力和滑动摩擦力，根据共点力平衡条件列式求解；
（2）对小球受力分析，受重力、风的推力、支持力和滑动摩擦力，根据牛顿第二定律列式求解出加速度，然后根据位移时间公式求解运动时间．
（2）对小球受力分析，受重力、风的推力、支持力和滑动摩擦力，根据牛顿第二定律列式求解出加速度，然后根据位移时间公式求解运动时间．
解答：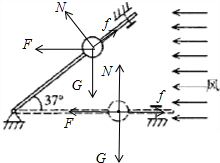
解：（1）设小球所受的风力为F，小球质量为m
F=μmg
故
μ=
=
=0.5
即小球与杆之间的动摩擦因素为0.5．
（2）设杆对小球的支持力为N，摩擦力为f
沿杆方向
F?cos37°+mgsin37°-f=ma
垂直于杆方向
N+Fsin37°-mgcos37°=0
其中：f=μN
可解得
a=
=（g+
）sinθ=
g
S=
at2
∴t═
=
即小球从静止出发在细杆上滑下距离S所需时间为
．
解：（1）设小球所受的风力为F，小球质量为mF=μmg
故
μ=
| F |
| mg |
| 0.5 mg |
| mg |
即小球与杆之间的动摩擦因素为0.5．
（2）设杆对小球的支持力为N，摩擦力为f
沿杆方向
F?cos37°+mgsin37°-f=ma
垂直于杆方向
N+Fsin37°-mgcos37°=0
其中：f=μN
可解得
a=
| Fcosθ+mgsinθ-f |
| m |
| F2 |
| m2g |
| 3 |
| 4 |
S=
| 1 |
| 2 |
∴t═
|
|
即小球从静止出发在细杆上滑下距离S所需时间为
|
点评：本题关键是对小球多次受力分析，结合正交分解法，根据牛顿第二定律列式求解．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
（2000?上海）如图所示为用频闪摄影方法拍摄的研究物体做平抛运动规律的照片．图中A、B、C为三个同时由同一点出发的小球．AA′为A球在光滑水平面上以速度υ运动的轨迹．BB′为B球以速度υ被水平抛出后的运动轨迹．CC′为C球自由下落的运动轨迹．通过分析上述三条轨迹可得出结论
（2000?上海）如图为一名宇航员“漂浮”在地球外层空间的照片，根据照片展现的情景提出两个与物理知识有关的问题（所提的问题可以涉及力学、电磁学、热学、光学、原子物理学等各个部分，只需提出问题，不必作出回答和解释）：
（2000?上海）如图所示，粗细均匀，两端开口的U形管竖直放置，管的内径很小，水平部分BC长14厘米，一空气柱将管内水银分隔成左右两段，大气压强相当于高为76厘米水银柱的压强．