题目内容
18.在一定高度处把一个小球以v0=30m/s的速度水平抛出,它落地时的速度大小为vt=50m/s,如果空气阻力不计,重力加速度g=10m/s2.求(1)小球在空中运动的时间t
(2)小球在平抛运动过程中通过的水平位移x和竖直位移y
(3)小球在平抛运动过程中的平均速度大小$\overline v$.
分析 (1)根据平抛运动的规律,小球在竖直方向做自由落体运动,将末速度分解求出竖直方向的分速度,然后根据v=gt求出时间;
(2)小球在水平方向做匀速运动,知道时间和初速度就可以求出小球运动的水平距离,根据$h=\frac{1}{2}g{t}^{2}$求出竖直方向的位移;
(3)求出小球的合位移,然后由平均速度的公式即可求出平均速度.
解答 解:(1)设小球落地时的竖直分速度为vy,由运动的合成可得${v_t}=\sqrt{{v_0}^2+{v_y}^2}$
解得 ${v_y}=\sqrt{{v_t}^2-{v_0}^2}=\sqrt{{{50}^2}-{{30}^2}}m/s=40m/s$
小球在竖直方向做自由落体运动,有vy=gt
解得 $t=\frac{v_y}{g}=\frac{40}{10}s=4s$
(2)小球在水平方向的位移为 x=v0t=30×4m=120m
小球的竖直位移为 $y=\frac{1}{2}g{t^2}=\frac{1}{2}×10×{4^2}m=80m$
(3)小球位移的大小为 $s=\sqrt{{x^2}+{y^2}}=\sqrt{{{120}^2}+{{80}^2}}m=40\sqrt{13}m$
由平均速度公式可得 $\overline v=\frac{s}{t}=\frac{{40\sqrt{13}}}{4}m/s=10\sqrt{13}m/s$
答:(1)小球在空中运动的时间是4s;
(2)小球在平抛运动过程中通过的水平位移是120m,竖直位移是80m;
(3)小球在平抛运动过程中的平均速度大小是$10\sqrt{13}$m/s.
点评 解决本题的关键是掌握平抛运动的性质,知道平抛运动如何分解,明确其运动时间是高度决定的.

练习册系列答案
相关题目
6.热核反应是一种理想能源的原因是( )
| A. | 就平均每一个核子来说,热核反应比重核裂变时释放的能量多 | |
| B. | 对环境的放射性污染较裂变轻,且较容易处理 | |
| C. | 热核反应的原料在地球上储量丰富 | |
| D. | 热核反应的速度容易控制 |
13.关于力对物体所做的功,下列说法正确的是( )
| A. | 滑动摩擦力对物体做功的多少与物体的路径无关 | |
| B. | 如果合外力对物体不做功,则物体必定做匀速直线运动 | |
| C. | 在相同时间内一对作用力与反作用力所做功的绝对值一定相等 | |
| D. | 一对作用力和反作用力,可能作用力做功,而反作用力不做功 |
3.下列说法正确的是( )
| A. | 竖直下抛运动是匀加速直线运动 | B. | 竖直下抛运动是自由落体运动 | ||
| C. | 竖直上抛运动是匀减速直线运动 | D. | 竖直上抛运动是匀加速直线运动 |
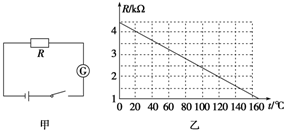 温度传感器广泛应用于室内空调、电冰箱和微波炉等家电产品中,它是利用热敏电阻的阻值随温度的变化而变化的特性工作的.如图甲中,电源的电动势E=9.0V,内电阻可忽略不计,G为灵敏电流表,内阻Rg 保持不变;R为热敏电阻,其电阻值与温度的变化关系如图乙的R-t图线所示,闭合开关,当R的温度等于20℃时,电流表示数I1=2mA.
温度传感器广泛应用于室内空调、电冰箱和微波炉等家电产品中,它是利用热敏电阻的阻值随温度的变化而变化的特性工作的.如图甲中,电源的电动势E=9.0V,内电阻可忽略不计,G为灵敏电流表,内阻Rg 保持不变;R为热敏电阻,其电阻值与温度的变化关系如图乙的R-t图线所示,闭合开关,当R的温度等于20℃时,电流表示数I1=2mA. 如图所示,可视为质点的两带电滑块A、B的电量均为+Q、质量均为m.A固定于粗糙绝缘的水平桌面上,将A、B的间距调节为d时B恰能静止在桌面上,已知重力加速度为g,设最大静摩擦力与滑动摩擦力相等.求:
如图所示,可视为质点的两带电滑块A、B的电量均为+Q、质量均为m.A固定于粗糙绝缘的水平桌面上,将A、B的间距调节为d时B恰能静止在桌面上,已知重力加速度为g,设最大静摩擦力与滑动摩擦力相等.求: 在“测定匀变速直线运动加速度”实验中,如图所示是小车作匀加速直线运动时,用打点计时器打出的一段纸带.若每相邻计数点的时间间隔T=0.1s,测得图中S1=2.00cm,S4=3.50cm,中间S2、S3的数据未测出.用上述数据计算小车加速度的公式为a=$\frac{s_4-s_1}{3T^2}$,并计算出小车的加速度大小为0.5m/s2.
在“测定匀变速直线运动加速度”实验中,如图所示是小车作匀加速直线运动时,用打点计时器打出的一段纸带.若每相邻计数点的时间间隔T=0.1s,测得图中S1=2.00cm,S4=3.50cm,中间S2、S3的数据未测出.用上述数据计算小车加速度的公式为a=$\frac{s_4-s_1}{3T^2}$,并计算出小车的加速度大小为0.5m/s2.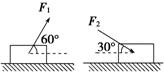 如图所示,一物块置于水平地面上.当用与水平方向成60°角的力F1拉物块时,物块做匀速直线运动;当改用与水平方向成30°角的力F2推物块时,物块仍做匀速直线运动.若F1是F2相等,求物块与地面之间的动摩擦因数.(用根式表示)
如图所示,一物块置于水平地面上.当用与水平方向成60°角的力F1拉物块时,物块做匀速直线运动;当改用与水平方向成30°角的力F2推物块时,物块仍做匀速直线运动.若F1是F2相等,求物块与地面之间的动摩擦因数.(用根式表示)