题目内容
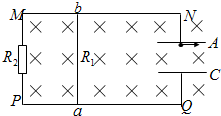 如图所示,MN和PQ是相距40cm的平行金属导轨,一根电阻R1=3Ω的金属棒ab可紧贴平行导轨运动,两块相互平行,相距20cm且水平放置的金属板A和C分别与两平行导轨相连接,图中跨接在ab间的电阻R2=1Ω,导轨和连接导线的电阻可忽略不计,先将整个装置放在图示的匀强磁场中,当导体棒ab以速率v匀速沿导轨运动时,能使一个质量为m、带电量为q的负电微粒也以速率v在两金属板空间做匀速圆周运动而不触及两板.求:
如图所示,MN和PQ是相距40cm的平行金属导轨,一根电阻R1=3Ω的金属棒ab可紧贴平行导轨运动,两块相互平行,相距20cm且水平放置的金属板A和C分别与两平行导轨相连接,图中跨接在ab间的电阻R2=1Ω,导轨和连接导线的电阻可忽略不计,先将整个装置放在图示的匀强磁场中,当导体棒ab以速率v匀速沿导轨运动时,能使一个质量为m、带电量为q的负电微粒也以速率v在两金属板空间做匀速圆周运动而不触及两板.求:(1)金属棒ab的运动方向.
(2)ab匀速运动速度的取值范围.
(3)若带电微粒在匀强磁场中从图所示开始运动,当运动位移达到
| ||
| Bq |
分析:(1)由题带电量为q的负电微粒做匀速圆周运动,所受重力与电场力平衡,则电场力方向竖直向上,电场强度方向下竖直向下,说明A板带正电,根据右手定则判断出金属棒ab的运动方向.
(2)ab匀速运动速度最大时,微粒在复合场中匀速圆周运动的半径最大为r=
=10cm.根据洛伦兹力提供向心力列方程,得到速度v与磁感应强度B的关系式.又由重力与电场力平衡列方程,两式联立,求解v,再求解范围.
(3)带电微粒在匀强磁场中圆周运动的半径r=
,当运动位移达到
=
r时微粒运动了
圆周,经过时间为t=
T,由圆周运动公式求解时间.
(2)ab匀速运动速度最大时,微粒在复合场中匀速圆周运动的半径最大为r=
| d |
| 2 |
(3)带电微粒在匀强磁场中圆周运动的半径r=
| mv |
| qB |
| ||
| Bq |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)由题带电量为q的负电微粒做匀速圆周运动,所受重力与电场力平衡,则电场力方向竖直向上,电场强度方向下竖直向下,说明A板带正电,金属棒ab的b端相当电源的正极,根据右手定则判断出金属棒ab的运动方向:水平向右.
(2)微粒在复合场中匀速圆周运动的半径最大为r=
=10cm.根据牛顿第二定律得
qvB=m
又qE=mg,E=
,U=
Blv
四式联立解得 v=
m/s
则ab匀速运动速度的取值范围:0<v≤
m/s.
(3)带电微粒在匀强磁场中圆周运动的周期T=
,当运动位移达到
=
r时微粒运动了
圆周,经过时间为t=
T=
.
答:(1)金属棒ab的运动方向为水平向右.
(2)ab匀速运动速度的取值范围为0<v≤
m/s.
(3)若带电微粒在匀强磁场中从图所示开始运动,当运动位移达到
时的时间为
.
(2)微粒在复合场中匀速圆周运动的半径最大为r=
| d |
| 2 |
qvB=m
| v2 |
| r |
又qE=mg,E=
| U |
| d |
| R1 |
| R1+R2 |
四式联立解得 v=
| 2 |
则ab匀速运动速度的取值范围:0<v≤
| 2 |
(3)带电微粒在匀强磁场中圆周运动的周期T=
| 2πm |
| qB |
| ||
| Bq |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| πm |
| 2qB |
答:(1)金属棒ab的运动方向为水平向右.
(2)ab匀速运动速度的取值范围为0<v≤
| 2 |
(3)若带电微粒在匀强磁场中从图所示开始运动,当运动位移达到
| ||
| Bq |
| πm |
| 2qB |
点评:本题涉及电磁感应、电路、电场、磁场和牛顿运动定律等多方面知识,考查综合应用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?天津模拟)如图所示,MN和PQ为固定在绝缘水平面上两平行光滑金属导轨,导轨左端MP间接有阻值为R1=2Ω导线;导轨右端接有与水平轨道相切、半径r=0.5m内壁光滑的半圆金属轨道.导轨间距L=0.4m,电阻不计.导轨所在平面abcd区域内有竖直向上B=0.5T的匀强磁场.导轨上长度也为0.4m、质量m=0.6kg、电阻R2=1Ω的金属棒AB以v0=6m/s速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触.已知重力加速度g=10m/s2.求:
(2013?天津模拟)如图所示,MN和PQ为固定在绝缘水平面上两平行光滑金属导轨,导轨左端MP间接有阻值为R1=2Ω导线;导轨右端接有与水平轨道相切、半径r=0.5m内壁光滑的半圆金属轨道.导轨间距L=0.4m,电阻不计.导轨所在平面abcd区域内有竖直向上B=0.5T的匀强磁场.导轨上长度也为0.4m、质量m=0.6kg、电阻R2=1Ω的金属棒AB以v0=6m/s速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触.已知重力加速度g=10m/s2.求: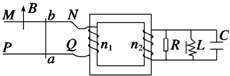 如图所示,MN和PQ为两个光滑的电阻不计的水平金属导轨,变压器为理想变压器,今在水平导轨部分加一竖直向上的匀强磁场,则以下说法正确的是( )
如图所示,MN和PQ为两个光滑的电阻不计的水平金属导轨,变压器为理想变压器,今在水平导轨部分加一竖直向上的匀强磁场,则以下说法正确的是( )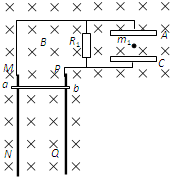 (2006?河东区二模)如图所示,MN和PQ是竖直放置相距1m的光滑平行金属导轨,(导轨足够长,电阻不计),其上方连有R1=9Ω的电阻和两块水平放置相距d=20cm的平行金属板,A、C,金属板长L=1m,将整个装置放置在如图所示的方向垂直纸面向里的匀强磁场中,磁感应强度B=1T,现使电阻R2=1Ω的金属棒ab与导轨MN、PQ接触,并由静止释放,当其下落h=10m时恰能匀速运动(运动中ab棒始终保持水平状态,且与导轨接触良好),此时将一质量m1=0.45g,带电荷量q=1.0×10-4C的微粒放置在A、C金属板的正中央,微粒恰好静止,(g=10m/s2,设两板间的电场为匀强电场),求:
(2006?河东区二模)如图所示,MN和PQ是竖直放置相距1m的光滑平行金属导轨,(导轨足够长,电阻不计),其上方连有R1=9Ω的电阻和两块水平放置相距d=20cm的平行金属板,A、C,金属板长L=1m,将整个装置放置在如图所示的方向垂直纸面向里的匀强磁场中,磁感应强度B=1T,现使电阻R2=1Ω的金属棒ab与导轨MN、PQ接触,并由静止释放,当其下落h=10m时恰能匀速运动(运动中ab棒始终保持水平状态,且与导轨接触良好),此时将一质量m1=0.45g,带电荷量q=1.0×10-4C的微粒放置在A、C金属板的正中央,微粒恰好静止,(g=10m/s2,设两板间的电场为匀强电场),求: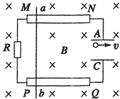 如图所示,MN和PQ是相距l=40cm的平行金属导轨,一根电阻r=0.3Ω的金属棒ab可紧贴平行导轨运动.两块相互平行,相距d=20cm,且水平放置的金属板A和C分别与两金属导轨相连接,图中跨接在两导轨间的电阻R=0.1Ω,导轨和连接导线的电阻均可忽略不计.现将整个装置放置在图示的匀强磁场中,当导体棒ab以速率v匀速沿导轨运动时,恰能使一个带负电的微粒也以速率v在两金属板间做匀速圆周运动.重力加速度g取10m/s2,求:
如图所示,MN和PQ是相距l=40cm的平行金属导轨,一根电阻r=0.3Ω的金属棒ab可紧贴平行导轨运动.两块相互平行,相距d=20cm,且水平放置的金属板A和C分别与两金属导轨相连接,图中跨接在两导轨间的电阻R=0.1Ω,导轨和连接导线的电阻均可忽略不计.现将整个装置放置在图示的匀强磁场中,当导体棒ab以速率v匀速沿导轨运动时,恰能使一个带负电的微粒也以速率v在两金属板间做匀速圆周运动.重力加速度g取10m/s2,求: