题目内容
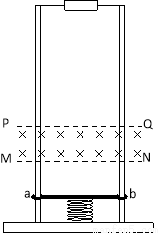
如图所示,质量均为m的物体A、B之间用劲度系数为K的轻弹簧连接,静止于倾角为θ的光滑斜面上,物体A与挡板接触而不粘连,物体R用平行于斜面的轻质细线绕过光滑的滑轮与水平导轨上的金属杆ab连接.金属杆ab、cd的质量都为m0,电阻都为R.金属杆长度及导轨的宽度均为d,金属杆与导轨的接触良好,水平导轨足够长且光滑,电阻不计,导轨间有垂直于导轨平面向上的匀强磁场(图中未画出)磁感应强度为B.开始时整个系统处于静止状态,与杆连接的细线水平,细线刚好拉直而无作用力.现用恒定的水平力作用于cd杆的中点,使杆cd由静止开始向右运动,当杆cd开始匀速运动时,物体A恰好与挡板间无弹力.求:
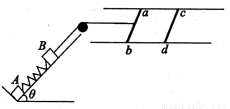
(1)从杆cd开始运动到匀速运动过程中物体B运动的距离L;
(2)cd杆匀速运动的速度大小v;
(3)从cd杆开始运动到匀速运动过程中,cd杆产生的焦耳热为Q,水平恒力做的功W为多大?
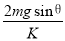
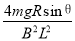

【解析】
试题分析:(1)弹簧开始时的压缩量为:x1=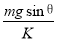 ,挡板恰无弹力时弹簧的伸长量为:x2=
,挡板恰无弹力时弹簧的伸长量为:x2= 则B移动距离为:L=x1+x2=
则B移动距离为:L=x1+x2=
(2)cd杆匀速运动时有:F=FA=2mgsinθ
又安培力为:FA=BIL
感应电流为:I=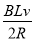
联立得:v=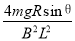
(3)由功能关系得:W=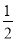 m0v2+mgLsinθ+Q热
m0v2+mgLsinθ+Q热
Q热=2Q

考点:本题考查导体切割磁感线时的感应电动势;功的计算.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目