题目内容
在如图所示的水平导轨(摩擦、电阻忽略不计)处于竖直向下的匀强磁场中,磁场的磁感强度B,导轨左端的间距为L1=4l0,右端间距为L2=4l0,两段导轨均足够长.今在导轨上放置AC、DE两根导体棒,质量分别为m1=2m0,m2=m0.电阻分别为R1=4R0,R2=R0.若AC棒以初速度v0向右运动,求:
(1)定性描述全过程中AC棒的运动情况
(2)两棒在达到稳定状态前加速度之比
是多少?
(3)运动过程中DE棒产生的总焦耳热QDE.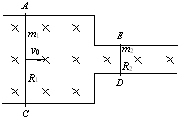
(1)定性描述全过程中AC棒的运动情况
(2)两棒在达到稳定状态前加速度之比
| a1 |
| a2 |
(3)运动过程中DE棒产生的总焦耳热QDE.

(1)A、C棒向右运动,回路中产生顺时针感应电流,AC棒受安培力的作用后减速;DE棒受安培力产生加速度向右运动,回路中磁通量的变化减慢,感应电流逐渐减小,因此两棒所受的安培力均减小,最终两棒产生的感应电动势大小相等,回路中感应电流为零,两棒不再受安培力,则知AC棒做加速度减小的减速运动,最终匀速运动,
(2)两棒达到稳定之前AC、DE棒中通过的电流大小始终相等,设加速度分别为a1和a2
根据牛顿第二定律得
a1=
=
a2=
=
又题意 m1=4m2 L1=4L2
解得
=
=
(3)两棒在达到稳定之前,回路中始终存在磁通量的变化,有感应电流就会产生焦耳热.当两棒运动速度满足一定关系时,回路中的磁通量不变,则总电动势为零,两棒均做匀速运动,不再产生热量.设两棒最终速度分别为v1、v2,取向右为正方向.则有
BL1v1=BL2v2 得 v1=
根据动量定理得:
对AC棒:-B
L1△t=m1△v
-∑B
L1△t=∑m1△vt
-B
L1△t=m1v1-m1v0
同理,对DE棒有:B
L2t=m2v2-0
解方程得:v1=
v2=
由于两棒串联,产生的焦耳热之比为
=
=
根据能量守恒定律得:QDE=
(
m1
-
m1
-
m2
)=
m0v
答:
(1)AC棒做加速度减小的减速运动,最终匀速运动,
(2)两棒在达到稳定状态前加速度之比
是
.
(3)运动过程中DE棒产生的总焦耳热QDE为
m0v
.
(2)两棒达到稳定之前AC、DE棒中通过的电流大小始终相等,设加速度分别为a1和a2
根据牛顿第二定律得
a1=
| F1 |
| m1 |
| BIL1 |
| m1 |
a2=
| F2 |
| m2 |
| BIL2 |
| m2 |
又题意 m1=4m2 L1=4L2
解得
| a1 |
| a2 |
| L1m2 |
| L2m1 |
| 2 |
| 1 |
(3)两棒在达到稳定之前,回路中始终存在磁通量的变化,有感应电流就会产生焦耳热.当两棒运动速度满足一定关系时,回路中的磁通量不变,则总电动势为零,两棒均做匀速运动,不再产生热量.设两棒最终速度分别为v1、v2,取向右为正方向.则有
BL1v1=BL2v2 得 v1=
| v2 |
| 4 |
根据动量定理得:
对AC棒:-B
| . |
| I |
-∑B
| . |
| I |
-B
| . |
| I |
同理,对DE棒有:B
| . |
| I |
解方程得:v1=
| v0 |
| 9 |
| 4v0 |
| 9 |
由于两棒串联,产生的焦耳热之比为
| QAC |
| QDE |
| R1 |
| R2 |
| 4 |
| 1 |
根据能量守恒定律得:QDE=
| 1 |
| 5 |
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
| 77 |
| 405 |
| 20 |
答:
(1)AC棒做加速度减小的减速运动,最终匀速运动,
(2)两棒在达到稳定状态前加速度之比
| a1 |
| a2 |
| 2 |
| 1 |
(3)运动过程中DE棒产生的总焦耳热QDE为
| 77 |
| 405 |
| 20 |

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 在如图所示的水平导轨上(摩擦、电阻忽略不计),有竖直向下的匀强磁场,磁感强度B,导轨左端的间距为L1=4L0,右端间距为L2=L0.今在导轨上放置AC,DE两根导体棒,质量分别为m1=2m0,m2=m0,电阻R1=4R0,R2=R0.若AC棒以初速度V0向右运动,求AC棒运动的过程中产生的总焦耳热QAC,以及通过它们的总电量q.
在如图所示的水平导轨上(摩擦、电阻忽略不计),有竖直向下的匀强磁场,磁感强度B,导轨左端的间距为L1=4L0,右端间距为L2=L0.今在导轨上放置AC,DE两根导体棒,质量分别为m1=2m0,m2=m0,电阻R1=4R0,R2=R0.若AC棒以初速度V0向右运动,求AC棒运动的过程中产生的总焦耳热QAC,以及通过它们的总电量q. (2007?南京一模)在如图所示的水平导轨(摩擦、电阻忽略不计)处于竖直向下的匀强磁场中,磁场的磁感强度B,导轨左端的间距为L1=4l0,右端间距为L2=4l0,两段导轨均足够长.今在导轨上放置AC、DE两根导体棒,质量分别为m1=2m0,m2=m0.电阻分别为R1=4R0,R2=R0.若AC棒以初速度v0向右运动,求:
(2007?南京一模)在如图所示的水平导轨(摩擦、电阻忽略不计)处于竖直向下的匀强磁场中,磁场的磁感强度B,导轨左端的间距为L1=4l0,右端间距为L2=4l0,两段导轨均足够长.今在导轨上放置AC、DE两根导体棒,质量分别为m1=2m0,m2=m0.电阻分别为R1=4R0,R2=R0.若AC棒以初速度v0向右运动,求:

