题目内容
如图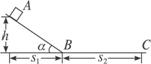
图
解析:我们可以将摩擦因数这一未知数包含在整个过程的摩擦力中,写出整个过程摩擦力的功的表达式,以及下滑过程重力做功的表达式,依据动能定理,两者总功等于滑块动能的变化,从而列方程求得动摩擦因数.
滑块从A滑向C的过程中,重力做正功(在斜面上WG=![]() =mgh),阻力(滑动摩擦力)做负功W,支持力不做功,且滑块的初动能(A点的动能)为零,末动能(C点的动能)也为零,设滑块质量为m,动摩擦因数为μ,斜面倾角为α,斜面底部长为s1,水平部分长为s2,由动能定理得
=mgh),阻力(滑动摩擦力)做负功W,支持力不做功,且滑块的初动能(A点的动能)为零,末动能(C点的动能)也为零,设滑块质量为m,动摩擦因数为μ,斜面倾角为α,斜面底部长为s1,水平部分长为s2,由动能定理得
mgh-μmgcosα·![]() -μmgs2=0
-μmgs2=0
即h-μs1-μs2=0
解得μ=![]() .
.

练习册系列答案
相关题目