题目内容
7.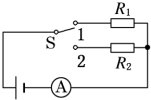 如图所示,定值电阻R1=10Ω,R2=8Ω,当开关S接“1”时,电流表示数为0.20A,那么当S接“2”时,电流表示数为0.24A.求电源的电动势和内阻.
如图所示,定值电阻R1=10Ω,R2=8Ω,当开关S接“1”时,电流表示数为0.20A,那么当S接“2”时,电流表示数为0.24A.求电源的电动势和内阻.
分析 对两种情况,分别运用闭合电路欧姆定律列式,然后联立方程组求解即可电源的电动势和内阻.
解答 解:由闭合电路欧姆定律可得:E=I(R+r)
对两种情况分别有:
E=I1(R1+r) ①
E=I2(R2+r) ②
代入数据得:
E=0.2(10+r)③
E=0.24(8+r)④
由③④联立解得 E=2.4V,r=2Ω
答:电源的电动势为2.4V,内阻为2Ω.
点评 本题关键对整个电路分两次运用闭合电路欧姆定律列式,然后联立方程组求解,本题提供的方法是实验中测量电源的电动势和内阻的基本方法:安阻法.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
17.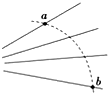 如图所示,实线是一个电场中的电场线,虚线是一个负的试探电荷,在这个电场中仅在电场力作用下的运动轨迹如图.若电荷是从a处运动到b处,以下判断正确的是( )
如图所示,实线是一个电场中的电场线,虚线是一个负的试探电荷,在这个电场中仅在电场力作用下的运动轨迹如图.若电荷是从a处运动到b处,以下判断正确的是( )
 如图所示,实线是一个电场中的电场线,虚线是一个负的试探电荷,在这个电场中仅在电场力作用下的运动轨迹如图.若电荷是从a处运动到b处,以下判断正确的是( )
如图所示,实线是一个电场中的电场线,虚线是一个负的试探电荷,在这个电场中仅在电场力作用下的运动轨迹如图.若电荷是从a处运动到b处,以下判断正确的是( )| A. | 电荷从a到b速度增大 | B. | 电荷从a到b加速度减小 | ||
| C. | 电荷从a到b电场力做负功 | D. | 电荷从a到b电势能减少 |
18. 如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a,平行板电容器AB内部原有电荷P处于静止状态,当两极板A和B的间距稍增大一些的瞬间(两极板仍平行),关于电荷P的说法正确的是( )
如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a,平行板电容器AB内部原有电荷P处于静止状态,当两极板A和B的间距稍增大一些的瞬间(两极板仍平行),关于电荷P的说法正确的是( )
 如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a,平行板电容器AB内部原有电荷P处于静止状态,当两极板A和B的间距稍增大一些的瞬间(两极板仍平行),关于电荷P的说法正确的是( )
如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a,平行板电容器AB内部原有电荷P处于静止状态,当两极板A和B的间距稍增大一些的瞬间(两极板仍平行),关于电荷P的说法正确的是( )| A. | 仍静止不动 | B. | 向下运动 | C. | 向上运动 | D. | 电荷P带正电 |
15.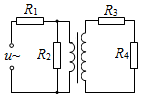 如图所示,理想变压器原、副线圈匝数比为1:2,两端分别接有四个阻值相同的定值电阻,变压器初级线圈接到交变电源上,下列说法正确的是( )
如图所示,理想变压器原、副线圈匝数比为1:2,两端分别接有四个阻值相同的定值电阻,变压器初级线圈接到交变电源上,下列说法正确的是( )
 如图所示,理想变压器原、副线圈匝数比为1:2,两端分别接有四个阻值相同的定值电阻,变压器初级线圈接到交变电源上,下列说法正确的是( )
如图所示,理想变压器原、副线圈匝数比为1:2,两端分别接有四个阻值相同的定值电阻,变压器初级线圈接到交变电源上,下列说法正确的是( )| A. | 副线圈电压是电源电压的2倍 | |
| B. | 流过R1的电流是副线圈上电流的2倍 | |
| C. | R1上的电功率是R2上电功率的2倍 | |
| D. | R1上的电功率是R2上电功率的9倍 |
2. 如图所示,A1、A2是理想电流表,V1、V2是理想电压表,电阻R1、R2、R3均为定值电阻,R4为滑动变阻器,G为灵敏电流计,不计内阻.当滑动变阻器R4的滑片向左移动一小段距离时,灵敏电流计的读数为零,下列说法正确的是( )
如图所示,A1、A2是理想电流表,V1、V2是理想电压表,电阻R1、R2、R3均为定值电阻,R4为滑动变阻器,G为灵敏电流计,不计内阻.当滑动变阻器R4的滑片向左移动一小段距离时,灵敏电流计的读数为零,下列说法正确的是( )
 如图所示,A1、A2是理想电流表,V1、V2是理想电压表,电阻R1、R2、R3均为定值电阻,R4为滑动变阻器,G为灵敏电流计,不计内阻.当滑动变阻器R4的滑片向左移动一小段距离时,灵敏电流计的读数为零,下列说法正确的是( )
如图所示,A1、A2是理想电流表,V1、V2是理想电压表,电阻R1、R2、R3均为定值电阻,R4为滑动变阻器,G为灵敏电流计,不计内阻.当滑动变阻器R4的滑片向左移动一小段距离时,灵敏电流计的读数为零,下列说法正确的是( )| A. | 滑动变阻器R4的滑片移动之前,$\frac{{R}_{1}}{{R}_{2}}>\frac{{R}_{3}}{{R}_{4}}$ | |
| B. | 电表A1、A2示数均变大 | |
| C. | 电表V1、V2示数均变小 | |
| D. | 电源的效率变小 |
12.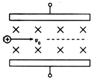 如图是一粒子速度选择器,两极间磁感应强度为B,电场强度为E,一速度为v0的电荷量为q的正离子(不计重力)恰能沿直线飞出速度选择器,则( )
如图是一粒子速度选择器,两极间磁感应强度为B,电场强度为E,一速度为v0的电荷量为q的正离子(不计重力)恰能沿直线飞出速度选择器,则( )
 如图是一粒子速度选择器,两极间磁感应强度为B,电场强度为E,一速度为v0的电荷量为q的正离子(不计重力)恰能沿直线飞出速度选择器,则( )
如图是一粒子速度选择器,两极间磁感应强度为B,电场强度为E,一速度为v0的电荷量为q的正离子(不计重力)恰能沿直线飞出速度选择器,则( )| A. | 若电荷量变为-q,其余条件不变,将往上偏 | |
| B. | 若速度变为2v0,其余条件不变,将往上偏 | |
| C. | 若速度变为$\frac{{v}_{0}}{2}$,其余条件不变,将往下偏 | |
| D. | 若改为+2q离子,其余条件不变,将往下偏 |
19.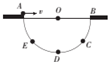 如图所示,有一半球形容器,其竖直截面为半圆.AB为沿水平方向的直径,D是圆周的最低点,E是AD间某一点,C与E在相同的高度.一个可视为质点的小球从A点以速度v0水平抛出,恰好落在E点,若以2v0抛出,恰好落在C点,设球的半径为R,则下列判断正确的是( )
如图所示,有一半球形容器,其竖直截面为半圆.AB为沿水平方向的直径,D是圆周的最低点,E是AD间某一点,C与E在相同的高度.一个可视为质点的小球从A点以速度v0水平抛出,恰好落在E点,若以2v0抛出,恰好落在C点,设球的半径为R,则下列判断正确的是( )
 如图所示,有一半球形容器,其竖直截面为半圆.AB为沿水平方向的直径,D是圆周的最低点,E是AD间某一点,C与E在相同的高度.一个可视为质点的小球从A点以速度v0水平抛出,恰好落在E点,若以2v0抛出,恰好落在C点,设球的半径为R,则下列判断正确的是( )
如图所示,有一半球形容器,其竖直截面为半圆.AB为沿水平方向的直径,D是圆周的最低点,E是AD间某一点,C与E在相同的高度.一个可视为质点的小球从A点以速度v0水平抛出,恰好落在E点,若以2v0抛出,恰好落在C点,设球的半径为R,则下列判断正确的是( )| A. | 初速度为$\frac{3{v}_{0}}{2}$时,小球恰好落在D点 | |
| B. | 初速度为$\frac{3{v}_{0}}{2}$时,小球将落在D点的左侧 | |
| C. | OC与竖直方向夹角的正弦值为$\frac{1}{4}$ | |
| D. | OE与竖直方向夹角的正弦值为$\frac{1}{3}$ |
16. 如图所示,A、B为两个等量同种电荷,a、0、b在点电荷A、B的连线上,C、O、d在连线的中垂线上Oa=Ob=Oc=Od,则( )
如图所示,A、B为两个等量同种电荷,a、0、b在点电荷A、B的连线上,C、O、d在连线的中垂线上Oa=Ob=Oc=Od,则( )
 如图所示,A、B为两个等量同种电荷,a、0、b在点电荷A、B的连线上,C、O、d在连线的中垂线上Oa=Ob=Oc=Od,则( )
如图所示,A、B为两个等量同种电荷,a、0、b在点电荷A、B的连线上,C、O、d在连线的中垂线上Oa=Ob=Oc=Od,则( )| A. | a、b两点的场强相同,电势也相同 | |
| B. | c、d两点的场强不相同,电势相同 | |
| C. | O点是A、B连线上电势最低的点,也是A、B连线上场强最小的点 | |
| D. | O点是中垂线cd上电势最高的点,也中垂线上场强最大的点 |
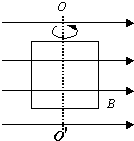 如图所示,把一个面积为4.0×10-2m2的单匝矩形线圈放在磁感应强度为2.0×10-2T的匀强磁场中,当线圈平面与磁场方向平行时,穿过线圈平面的磁通量为0Wb;当线圈绕OO′轴转动至与磁场方向垂直时,穿过线圈平面的磁通量为8×10-4Wb;在此转动过程中,穿过线圈平面的磁通量变大•(填“大”或“小”)
如图所示,把一个面积为4.0×10-2m2的单匝矩形线圈放在磁感应强度为2.0×10-2T的匀强磁场中,当线圈平面与磁场方向平行时,穿过线圈平面的磁通量为0Wb;当线圈绕OO′轴转动至与磁场方向垂直时,穿过线圈平面的磁通量为8×10-4Wb;在此转动过程中,穿过线圈平面的磁通量变大•(填“大”或“小”)