题目内容
[物理——选修3-5](15分)
(1)(5分)用频率为 的光照射大量处于基态的氢原子,在所发射的光谱中仅能观测到频率分别为
的光照射大量处于基态的氢原子,在所发射的光谱中仅能观测到频率分别为 的三条谱线,且
的三条谱线,且 ,则 。(填入正确选项前的字母)
,则 。(填入正确选项前的字母)
(2)(10分)如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙。重物质量为木板质量的2倍,重物与木板间的动摩擦因数为 。使木板与重物以共同的速度
。使木板与重物以共同的速度 向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。求木板从第一次与墙碰撞到再次碰撞所经历的时间。设木板足够长,重物始终在木板上。重力加速度为g。
向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。求木板从第一次与墙碰撞到再次碰撞所经历的时间。设木板足够长,重物始终在木板上。重力加速度为g。
(1)(5分)用频率为
 的光照射大量处于基态的氢原子,在所发射的光谱中仅能观测到频率分别为
的光照射大量处于基态的氢原子,在所发射的光谱中仅能观测到频率分别为 的三条谱线,且
的三条谱线,且 ,则 。(填入正确选项前的字母)
,则 。(填入正确选项前的字母)A. | B. | C. | D. |
 。使木板与重物以共同的速度
。使木板与重物以共同的速度 向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。求木板从第一次与墙碰撞到再次碰撞所经历的时间。设木板足够长,重物始终在木板上。重力加速度为g。
向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。求木板从第一次与墙碰撞到再次碰撞所经历的时间。设木板足够长,重物始终在木板上。重力加速度为g。
(1)B
(2)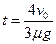
(2)
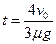
(1)本题考查的是能级跃迁的能量计算,能级跃迁时的能量大小为hυ,根据跃迁时的总能量不变得hυ3=hυ2+hυ1,则υ3=υ2+υ1,B项正确。
(2)本题考查的是动量守恒定律和动量定理。明确运动过程的初末状态是解题的关键。
第一次与墙碰撞后,木板的速度反向,大小不变,此后木板向左做匀减速运动,重物向右做匀减速运动,最后木板和重物达到共同的速度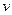 。设木板的质量为m,重物的质量为2m,取向右为动量的正向,由动量守恒得
。设木板的质量为m,重物的质量为2m,取向右为动量的正向,由动量守恒得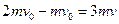 ①
①
设从第一次与墙碰撞到重物和木板具有共同速度v所用的时间为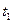 ,对木板应用动量定理得
,对木板应用动量定理得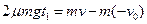 ②
②
由牛顿第二定律得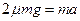 ③
③
式中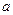 为木板的加速度。
为木板的加速度。
在达到共同速度v时,木板离墙的距离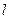 为
为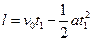 ④
④
开始向右做匀速运动到第二次与墙碰撞的时间为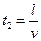 ⑤
⑤
从第一次碰撞到第二次碰撞所经过的时间为 ⑥
⑥
由以上各式得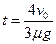 ⑦
⑦
(2)本题考查的是动量守恒定律和动量定理。明确运动过程的初末状态是解题的关键。
第一次与墙碰撞后,木板的速度反向,大小不变,此后木板向左做匀减速运动,重物向右做匀减速运动,最后木板和重物达到共同的速度
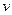 。设木板的质量为m,重物的质量为2m,取向右为动量的正向,由动量守恒得
。设木板的质量为m,重物的质量为2m,取向右为动量的正向,由动量守恒得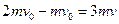 ①
①设从第一次与墙碰撞到重物和木板具有共同速度v所用的时间为
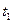 ,对木板应用动量定理得
,对木板应用动量定理得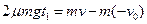 ②
②由牛顿第二定律得
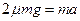 ③
③式中
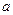 为木板的加速度。
为木板的加速度。在达到共同速度v时,木板离墙的距离
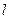 为
为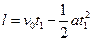 ④
④开始向右做匀速运动到第二次与墙碰撞的时间为
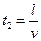 ⑤
⑤从第一次碰撞到第二次碰撞所经过的时间为
 ⑥
⑥由以上各式得
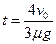 ⑦
⑦
练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 T,方向垂直纸面向里。开始时,将小物体P无初速释放,当P运动至Q处时,与静止在该处的小物体Q相碰,碰撞中Q的电荷量保持不变(即不转移)。碰撞后,两物体能够再次相遇。斜面无限长,g取10m/s2。求:
T,方向垂直纸面向里。开始时,将小物体P无初速释放,当P运动至Q处时,与静止在该处的小物体Q相碰,碰撞中Q的电荷量保持不变(即不转移)。碰撞后,两物体能够再次相遇。斜面无限长,g取10m/s2。求:
 =0.5,A、B、C均可视为质点,重力加速度为g.
=0.5,A、B、C均可视为质点,重力加速度为g. 一段时间A与C相碰,设碰撞时间极短,碰后一起压缩弹簧,弹簧最大压缩量为
一段时间A与C相碰,设碰撞时间极短,碰后一起压缩弹簧,弹簧最大压缩量为 L,求弹簧的最大弹性势能。
L,求弹簧的最大弹性势能。




