题目内容
（2011?潮州二模）地球同步通信卫星和月球都看做绕地球做匀速圆周运动，其圆周运动的向心力分别为F1、F2； 圆周运动速率分别为v1、v2； 向心加速度分别为a1、a2，则（ ）
分析：根据万有引力提供向心力，计算出向心力、速率和向心加速度的表达式进行讨论．
解答：解：A、对于地球卫星，万有引力提供向心力，设卫星的质量为m、轨道半径为r、地球质量为M，有
F=F向
F=G
F向=m
=mω2r=m（
）2r
因而
G
=m
=mω2r=m（
）2r=ma
解得
F向=
v=
ω=
T=
=2π
a=
根据F=G
，由于月球是天体，质量远大于同步卫星质量，半径相差没有这么明显，故F1＜F2，故A正确；
B、由于同步卫星的公转周期小于月球的公转周期，根据T=2π
，可知同步卫星的轨道半径小于月球的轨道半径，即
r1＜r2
根据v=
，v1＞v2，故B错误；
C、根据a=
，a1＞a2，故B错误；
D、根据v=
，v1＞v2＞
=7.9km/s，故D正确；
故选AD．
F=F向
F=G
| Mm |
| r2 |
F向=m
| v2 |
| r |
| 2π |
| T |
因而
G
| Mm |
| r2 |
| v2 |
| r |
| 2π |
| T |
解得
F向=
| 4π2r |
| T2 |
v=
|
ω=
|
T=
| 2πr |
| v |
|
a=
| GM |
| r2 |
根据F=G
| Mm |
| r2 |
B、由于同步卫星的公转周期小于月球的公转周期，根据T=2π
|
r1＜r2
根据v=
|
C、根据a=
| GM |
| r2 |
D、根据v=
|
|
故选AD．
点评：本题关键根据卫星的万有引力定律提供向心力，求解出周期、线速度和加速度表达式讨论．
练习册系列答案
阅读快车系列答案
相关题目
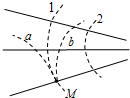（2011?潮州二模）如图所示，实线为方向未知的三条电场线，虚线1和2为等势线．a、b两个带电量相同的粒子以相同的速度从电场中M点沿等势线1的切线飞入，粒子仅在电场力作用下的运动轨迹如图中虚线所示，则在开始运动的一小段时间内（粒子在图示区域内）（ ）