题目内容
（13分）一质量为M＝1.0 kg的小物块随足够长的水平传送带一起运动，被一水平向左
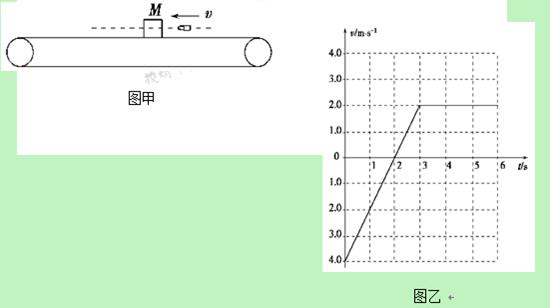
飞来的子弹击中并从物块中穿过，如图甲所示。地面观察者记录了物块被击中后的速度
随时间变化的关系如图乙所示，图中取向右运动的方向为正方向。已知传送带的速度保
持不变，g取10 m/s2。
（1）指出传送带速度v0的方向及大小，说明理由；
（2）计算物块与传送带间的动摩擦因数μ ；
（3）计算t=0开始物块与传送带之间由于摩擦而产生的内能Q。
【答案】
（13分）解：（1）从v-t图象看出，物块被击穿后，先向左减速到v=0，然后向右加速到v=2.0 m/s，以
后随传送带一起做匀速运动，所以，传送带的速度方向向右，其速度v0=2.0 m/s。 （3分）
（2）由速度图象可得，物块在滑动摩擦力的作用下做匀变速运动的加速度为a，
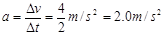（2分）
由牛顿第二定律得，滑动摩擦力Ff＝μMg=Ma
物块与传送带间的动摩擦因数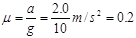 
（2分）
（3）由速度图象可知，传送带与物块存在摩擦力的时间只有3秒，
0~2s内：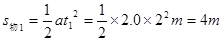
（向左） 
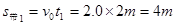（向右）
2~3s内：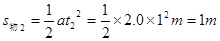
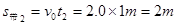（向右） 
（向右）
所以，物块与传送带之间的相对位移 ΔS相 = 4＋4＋2－1 = 9m （4分）
产生的内能 Q＝Ff S相 = μMg S相 = 0.2×1.0×10×9 = 18J （2分）
（本题应用功能关系求解正确的同样得分）
【解析】
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
