题目内容
OA杆是机器带动绕其轴线旋转的竖直杆，细绳的一端固定在杆的A点，另一端系一质量m="1" kg的小球，绳长为L="1" m.开始小球绕轴线在水平面内做匀速圆周运动，细绳与竖直杆的夹角为θ1=30°.现使机器转速加大，使小球在另一水平面内做稳定的匀速圆周运动时，细绳与竖直杆的夹角为θ2=60°.求此过程中机器对小球所做的功.（取g="10" m/s2）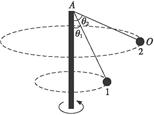
W机≈9.72 J
（1）设摆角为θ时，小球角速度为ω,绳中张力为T，则
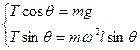
ω2=
.
（2）小球动能
Ek=
mv2=mω2(lsinθ)2=mgl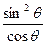
（3）由状态1到2：对小球，由动能定理
WG+W机=ΔEk
-mgl(cosθ1-cosθ2)+W机=mgl(
-
)
则W机=mgl(cosθ1-cosθ2)+
mgl(-)=10×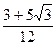
J=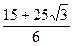
J≈9.72 J.
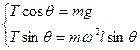
ω2=
.（2）小球动能
Ek=
mv2=mω2(lsinθ)2=mgl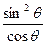（3）由状态1到2：对小球，由动能定理
WG+W机=ΔEk
-mgl(cosθ1-cosθ2)+W机=
mgl(-)则W机=mgl(cosθ1-cosθ2)+
mgl(-)=10×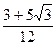J=
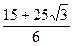J≈9.72 J.
练习册系列答案
阅读快车系列答案
相关题目
，B球质量为
，过杆的中点O有一水平光滑固定轴，杆可绕轴在竖直平面内转动。当转动到竖直位置且A球在上端，B球在下端时杆的角速度为ω，此时杆对转轴的作用力为零，则A、B两小球的质量之比为（ ）
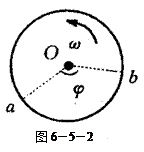
匀速转动，转动角速度
="2.5" rad/s，桶壁上P处有一圆孔，桶璧很薄，桶的半径R=2m。当圆孔运动到桶的上方时,在圆孔的正上方h=3.2m处有一个小球由静止开始下落，已知圆孔的半径略大于小球的半径。试通过计算判断小球是否和圆桶碰撞（不考虑空气阻力，g=10
）
