题目内容
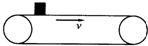
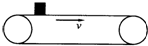 如图:一水平传送带以4m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由一端运动到另一端所经历的时间为6s,则物体与传送带之间的摩擦系数是多少?如果需要在最短的时间内把静止的物体从左端传送到右端,则传送带的速度至少应该是多少?
如图:一水平传送带以4m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由一端运动到另一端所经历的时间为6s,则物体与传送带之间的摩擦系数是多少?如果需要在最短的时间内把静止的物体从左端传送到右端,则传送带的速度至少应该是多少?分析:对物体受力分析,可知物体先匀加速运动,后匀速运动,根据运动学基本公式可以求得加速度,再根据牛顿第二定律求得摩擦系数;为使物体从A至B所用时间最短,物体必须始终处于加速状态,由于物体与传送带之间的滑动摩擦力不变,所以其加速度也不变,根据匀变速运动基本公式即可求解.
解答:解:物体放到传送带上,刚开始一段时间物体相对传送带向后滑动,但相对地向前运动.选取地面为参照物,物体在传送带的滑动摩擦力作用下从静止开始做匀加速直线运动,
其加速度为:a=
=μg
当物体的速度达到传送带的速度4m/s,物体与传送带无相对运动及相对运动趋势,故两者相对静止,物体一直以4m/s速度匀速运动到另一端.此时对地的位移是20m 物体开始做匀加速运动的时间为:
t1=
=
匀加速直线运动的时间为:
t2=6-
由运动学公式得:
S1+S2=S
at12+vt2=20m
解得:μ=0.2
为使物体从A至B所用时间最短,物体必须始终处于加速状态,由于物体与传送带之间的滑动摩擦力不变,所以其加速度也不变.
仍为:a=μg=0.2×10m/s2=2m/s2
设物体从A至B所用最短的时间为T,则:
aT2=S
得:T=2
s
所以传送带应具有的最小速率为:
vmin=aT=4
m/s
答:物体与传送带之间的摩擦系数是μ=0.2;如果需要在最短的时间内把静止的物体从左端传送到右端,则传送带的速度至少应该是4
m/s
其加速度为:a=
| μmg |
| m |
当物体的速度达到传送带的速度4m/s,物体与传送带无相对运动及相对运动趋势,故两者相对静止,物体一直以4m/s速度匀速运动到另一端.此时对地的位移是20m 物体开始做匀加速运动的时间为:
t1=
| v |
| a |
| 4 |
| μg |
匀加速直线运动的时间为:
t2=6-
| 4 |
| μg |
由运动学公式得:
S1+S2=S
| 1 |
| 2 |
解得:μ=0.2
为使物体从A至B所用时间最短,物体必须始终处于加速状态,由于物体与传送带之间的滑动摩擦力不变,所以其加速度也不变.
仍为:a=μg=0.2×10m/s2=2m/s2
设物体从A至B所用最短的时间为T,则:
| 1 |
| 2 |
得:T=2
| 5 |
所以传送带应具有的最小速率为:
vmin=aT=4
| 5 |
答:物体与传送带之间的摩擦系数是μ=0.2;如果需要在最短的时间内把静止的物体从左端传送到右端,则传送带的速度至少应该是4
| 5 |
点评:物体在传送带运动问题,关键是分析物体的受力情况,来确定物体的运动情况,有利于培养学生分析问题和解决问题的能力.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 如图:一水平传送带以2m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由左端运动到右端所经历的时间为11s,则:
如图:一水平传送带以2m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由左端运动到右端所经历的时间为11s,则: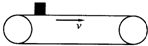 如图:一水平传送带以2m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由左端运动到右端所经历的时间为11s,则:
如图:一水平传送带以2m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由左端运动到右端所经历的时间为11s,则: