题目内容
6.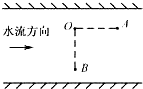 如图所示,甲、乙两同学从河中O点出发,分别沿直线游到A点和B点后,立即沿原路线返回到O点,OA、OB分别与水流方向平行和垂直.若水流速度不变,两人在静水中游速相等,且他们所用时间t甲=t乙,则OA和OB的关系为( )
如图所示,甲、乙两同学从河中O点出发,分别沿直线游到A点和B点后,立即沿原路线返回到O点,OA、OB分别与水流方向平行和垂直.若水流速度不变,两人在静水中游速相等,且他们所用时间t甲=t乙,则OA和OB的关系为( )| A. | OA<OB | B. | OA=OB | C. | OA>OB | D. | 无法确定 |
分析 甲、乙两同学实际的速度是静水中的流速与水流速度的合速度,设游速为v,水速为v0根据速度合成可知:甲游到A点的速度为v+v0,游回的速度为v-v0;乙来回的速度都为$\sqrt{{v}^{2}-{v}_{0}^{2}}$.明确了各自的合速度后,再用匀速直线运动规律求出时间进行比较.
解答  解:设游速为v,水速为v0,
解:设游速为v,水速为v0,
则甲整个过程所用时间:t甲=$\frac{OA}{v+{v}_{0}}$+$\frac{OA}{v-{v}_{0}}$,
乙为了沿OB运动,速度合成如图:
则乙整个过程所用时间:t乙=$\frac{OB}{\sqrt{{v}^{2}-{v}_{0}^{2}}}$×2,
因所用时间t甲=t乙,则有OA<OB,故A正确,BCD错误.
故选:A.
点评 本题考查运动的合成(主要是速度的合成)和匀速运动规律,运用速度合成的矢量平行四边形法则求出各自的合速度是关键.

练习册系列答案
相关题目
16.河宽为d,水流速度为v1,船在静水中的速度为v2,要使船在渡河过程中通过位移s最短,则下列说法正确的是( )
| A. | v1>v2时,s=d | B. | v1<v2时,s<d | C. | v1>v2时,s>d | D. | v1<v2时,s=d |
17.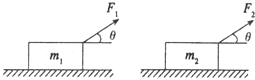 如图所示,质量分别为m1和m2的两个物体,在相同的两个力F1和F2作用下,沿水平方向移动了相同的距离,若F1做的功为W1,F2做的功为W2,且m1<m2,则( )
如图所示,质量分别为m1和m2的两个物体,在相同的两个力F1和F2作用下,沿水平方向移动了相同的距离,若F1做的功为W1,F2做的功为W2,且m1<m2,则( )
 如图所示,质量分别为m1和m2的两个物体,在相同的两个力F1和F2作用下,沿水平方向移动了相同的距离,若F1做的功为W1,F2做的功为W2,且m1<m2,则( )
如图所示,质量分别为m1和m2的两个物体,在相同的两个力F1和F2作用下,沿水平方向移动了相同的距离,若F1做的功为W1,F2做的功为W2,且m1<m2,则( )| A. | W1>W2 | B. | W1<W2 | ||
| C. | W1=W2 | D. | 条件不足,无法判断 |
14.一质量为m的木块静止在光滑的水平面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在t=t1时刻物体的( )
| A. | 速度为$\frac{F{t}_{1}}{m}$ | B. | 速度为$\frac{F{t}_{1}}{2m}$ | ||
| C. | 动能为$\frac{{F}^{2}{t}_{1}}{2m}$ | D. | 动能为$\frac{{F}^{2}{{t}_{1}}^{2}}{2m}$ |
1.对于曲线运动,下列说法中正确的是( )
| A. | 速度方向可能不变 | B. | 加速度一定是变化 | ||
| C. | 速度方向和加速度方向不可能一致 | D. | 合外力一定与速度方向垂直 |
11.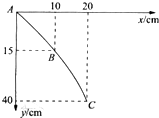 如图是小球做平抛运动的一段运动轨迹,A、B、C为运动轨迹上的三点,以A为坐标原点,建立坐标系,各点坐标值已在图中标出点在轨迹上,取重力加速度g=10m/s2,则小球做平抛运动的初速度为( )
如图是小球做平抛运动的一段运动轨迹,A、B、C为运动轨迹上的三点,以A为坐标原点,建立坐标系,各点坐标值已在图中标出点在轨迹上,取重力加速度g=10m/s2,则小球做平抛运动的初速度为( )
 如图是小球做平抛运动的一段运动轨迹,A、B、C为运动轨迹上的三点,以A为坐标原点,建立坐标系,各点坐标值已在图中标出点在轨迹上,取重力加速度g=10m/s2,则小球做平抛运动的初速度为( )
如图是小球做平抛运动的一段运动轨迹,A、B、C为运动轨迹上的三点,以A为坐标原点,建立坐标系,各点坐标值已在图中标出点在轨迹上,取重力加速度g=10m/s2,则小球做平抛运动的初速度为( )| A. | 0.5m/s | B. | 1m/s | C. | 1.5m/s | D. | 2m/s |
18.质量为1kg的物体从离地面5m高处自由下落.与地面碰撞后静止,设球与地面作用时间为0.2s,则小球对地面的平均冲力为(g=10m/s2)( )
| A. | 30N | B. | 60N | C. | 80N | D. | 100N |
4.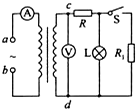 如图所示,理想变压器原线圈a、b两端接正弦交变电压u=220$\sqrt{2}$sin100πt(V),原、副线圈的匝数比n1:n2=10:1,电压表接在副线圈c、d两端,输电线的等效电阻为R,原来开关S是断开的,则当S闭合后,下列说法正确的是( )
如图所示,理想变压器原线圈a、b两端接正弦交变电压u=220$\sqrt{2}$sin100πt(V),原、副线圈的匝数比n1:n2=10:1,电压表接在副线圈c、d两端,输电线的等效电阻为R,原来开关S是断开的,则当S闭合后,下列说法正确的是( )
 如图所示,理想变压器原线圈a、b两端接正弦交变电压u=220$\sqrt{2}$sin100πt(V),原、副线圈的匝数比n1:n2=10:1,电压表接在副线圈c、d两端,输电线的等效电阻为R,原来开关S是断开的,则当S闭合后,下列说法正确的是( )
如图所示,理想变压器原线圈a、b两端接正弦交变电压u=220$\sqrt{2}$sin100πt(V),原、副线圈的匝数比n1:n2=10:1,电压表接在副线圈c、d两端,输电线的等效电阻为R,原来开关S是断开的,则当S闭合后,下列说法正确的是( )| A. | 电压表示数为22$\sqrt{2}$V | B. | 灯泡L的亮度变暗 | ||
| C. | 输电线上损耗的功率减小 | D. | 电流表示数变小 |