题目内容
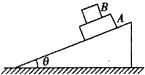 如图所示,两个重叠在一起的滑块,置于固定的倾角为θ的斜面上,滑块A和滑块B的质量分别为M和m.A与斜面间的摩擦系数为μ1,A和B间摩擦系数为μ2,两滑块都从静止开始,以相同的加速度沿斜面下滑,在这个过程中滑块B受的摩擦力( )
如图所示,两个重叠在一起的滑块,置于固定的倾角为θ的斜面上,滑块A和滑块B的质量分别为M和m.A与斜面间的摩擦系数为μ1,A和B间摩擦系数为μ2,两滑块都从静止开始,以相同的加速度沿斜面下滑,在这个过程中滑块B受的摩擦力( )分析:先以整体为研究对象,根据牛顿第二定律求出加速度,再以B为研究对象,根据牛顿第二定律求解B所受的摩擦力.
解答:解:
A、以整体为研究对象,根据牛顿第二定律得:
加速度a=
=g(sinθ-μ1cosθ)
设A对B的摩擦力为f,则有
mgsinθ+f=ma,得到f=ma-mgsinθ=-μ1mgcosθ,负号表示摩擦力方向沿斜面向上.
故ABC错误,D正确
故选:D
A、以整体为研究对象,根据牛顿第二定律得:
加速度a=
| (M+m)gsinθ-μ1(M+m)gcosθ |
| M+m |
设A对B的摩擦力为f,则有
mgsinθ+f=ma,得到f=ma-mgsinθ=-μ1mgcosθ,负号表示摩擦力方向沿斜面向上.
故ABC错误,D正确
故选:D
点评:本题是两个物体的连接体问题,要灵活选择研究对象,往往采用整体法和隔离法相结合的方法研究.

练习册系列答案
相关题目
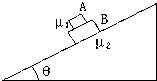 如图所示,两个重叠在一起的滑块置于固定的倾角为θ的斜面上,设A和B的质量分别为m和M,A与B间的动摩擦因数为μ1,B与斜面间的动摩擦因数为μ2,两滑块都从静止开始以相同的加速度沿斜面下滑,在这过程中说法正确的是( )
如图所示,两个重叠在一起的滑块置于固定的倾角为θ的斜面上,设A和B的质量分别为m和M,A与B间的动摩擦因数为μ1,B与斜面间的动摩擦因数为μ2,两滑块都从静止开始以相同的加速度沿斜面下滑,在这过程中说法正确的是( )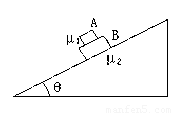
 的光滑斜面上,设A、B质量分别为m、M,A与B间的动摩擦因数为
的光滑斜面上,设A、B质量分别为m、M,A与B间的动摩擦因数为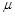 .两滑块保持相对静止沿斜面下滑,在这过程中,A受到的摩擦力为
.
.两滑块保持相对静止沿斜面下滑,在这过程中,A受到的摩擦力为
.