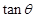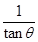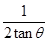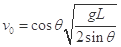题目内容
AB为半圆弧ACB的水平直径,C为ACB弧的中点,AB=1.5m,从A点平抛出一小球,小球下落0.3s后落到ACB上,则小球抛出的初速度v0为(g取10m/s2)( )
| A.1.5m/s | B.0.5m/s | C.3m/s | D.4.5m/s |
BD
解析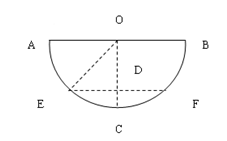
试题分析:据题意,物体下落时间为t=0.3s,则下落高度为hOD=gt2/2=0.45m,则可以肯定物体可能落在E、F两点,由于OE=0.75m,所以据勾股定理可得DE=0.6m;如果物体落在E点,则平抛运动的水平距离为x1=AO-ED=0.15m,则水平速度为v1= x1/t=0.5m/s;如果物体落在F点,则物体平抛的水平距离为x2=1.35m,则平抛速度为v2= x2/t=4.5m/s,所以BD选项正确。
考点:本题考查对平抛运动的应用,其中涉及几何关系和勾股定理。

如图.x轴在水平地面内.y轴沿竖直方向。图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的。不计空气阻力,则( )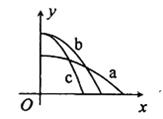
| A.a的飞行时间比b的长 |
| B.b和c的飞行时间相同 |
| C.a的水平速度比b的小 |
| D.b的初速度比c的小 |
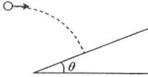
如图所示,从倾角为θ的斜面上的某点先后将同一小球以不同初速度水平抛出,小球均落到斜面上,当抛出的速度为v1时,小球到达斜面时的速度方向与斜面的夹角为α1,当抛出的速度为v2时,小球到达斜面时的速度方向与斜面的夹角为α2,则( )
| A.当v1>v2时,α1>α2 |
| B.当v1>v2时,α1<α2 |
| C.无论v1、v2大小如何,均有α1=α2 |
| D.2tanθ>tan(α1+θ) |
在一次救灾活动中,从水平飞行的直升机上投掷救灾物资。设飞机水平飞行的速度为v0,离地面高度为h,则当物资的速度方向与水平方向成θ时,物资的水平位移x与竖直位移y的关系为(不计空气阻力)
| A.x=ytanθ |
| B.x=2ytanθ |
C.x=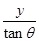 |
D.x=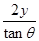 |
(多选)平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间大于2t1,下列说法中正确的是( )
| A.图线2表示竖直分运动的v-t图线 |
| B.t1时刻的速度方向与初速度方向夹角为30° |
| C.t1时间内的竖直位移与水平位移之比为1∶2 |
| D.2t1时刻的速度方向与初速度方向夹角为60° |
如题图所示的直角三角板紧贴在固定的刻度尺上方,使三角板沿刻度尺水平向右匀速运动的同时,一支铅笔从三角板直角边的最下端由静止开始沿此边向上做匀加速直线运动.下列关于铅笔笔尖的运动及其所留下的痕迹的判断中正确的是
| A.笔尖留下的痕迹是一条抛物线 |
| B.笔尖留下的痕迹是一条倾斜的直线 |
| C.在运动过程中,笔尖运动的速度方向时刻不变 |
| D.在运动过程中,笔尖运动的加速度方向时刻改变 |
在同一水平直线上的两位置分别沿同方向水平抛出两小球A和B,其运动轨迹如图,不计阻力,要使两球在空中相遇,则必须( )
| A.先抛出A球 | B.先抛出B球 |
| C.同时抛出两球 | D.A球的初速度小于B球的初速度 |
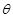 的斜面上时,其速度方向与斜面垂直,运动轨迹如右图中虚线所示。小球在竖直方向下落的距离与在水平方向通过的距离之比为( )
的斜面上时,其速度方向与斜面垂直,运动轨迹如右图中虚线所示。小球在竖直方向下落的距离与在水平方向通过的距离之比为( )