Question

如图所示，拉B物的轻绳与竖直方向成60°角，O为一定滑轮，物体A与B间用跨过定滑轮的细绳相连且均保持静止，已知物体B的重力为100N，物体A的重力为40N，绳和滑轮的摩擦及质量均不计，试求：
（1）水平地面对B的支持力的大小和方向；
（2）地面对物体B的摩擦力的大小和方向；
（3）求OP绳对滑轮的拉力大小．

Answer 1

分析：对A受力分析由平衡条件求出绳子的拉力，再对B受力分析，正交分解根据平衡条件列方程求出B受到的支持力及摩擦力；
以滑轮为研究对象受力分析，根据平衡条件求绳子PO的拉力．

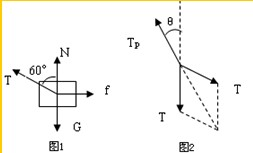
解答：解：（1）对物体B受力分析如图1，由物体B的受力平衡可得：Tcos60°+N=G
物体A所受的重力大小等于绳子的拉力：G_A=T
解得：N=80N
方向竖直向上

（2）地面对物体B的摩擦力为f，由平衡条件可知：f=Tsin60°
解得：f=20

3

N
方向水平向右
（3）对滑轮受力分析如图2：
OP的拉力为T_P，连接物体A、B的绳子拉力相等，由几何关系可知θ=30°
由力的合成可得T_p=2Tcosθ
解得：Tp=40

3

N
答：（1）水平地面对B的支持力的大小为80N，方向竖直向上；
（2）地面对物体B的摩擦力的大小为20

3

N，方向水平向右；
（3）OP绳对滑轮的拉力大小为40

3

N．

点评：本题关键是先对A受力分析，然后得到绳子BO的拉力大小；然后对物体B受力分析，根据平衡条件得到摩擦力和支持力；最后对滑轮分析，运用平衡条件，并根据合成法得到绳子PO的拉力．