题目内容
16.“嫦娥一号”探月卫星与稍早日本的“月亮女神号”探月卫星不同,“嫦娥一号”卫星是在绕月极地轨道上运动的,加上月球的自转,因而“嫦娥一号”卫星能探测到整个月球的表面,“嫦娥一号”卫星的CCD相继对月球背面进行成像检测,并获取了月球背面部分区域的影像图.卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地球公转的周期为TE,半径为Ro,地球半径为RE,月球半径为RM.若忽略地球及太阳引力对绕月卫星的影响,试求月球与地球质量之比为( )| A. | ($\frac{{T}_{E}}{{T}_{M}}$)2•($\frac{{R}_{M}+H}{{R}_{0}}$)3 | B. | $\frac{{{R}_{0}}^{3}{T}^{2}}{{{R}_{E}}^{3}{{T}_{0}}^{2}}$ | ||
| C. | $\frac{R{{E}_{K}}^{3}}{{{R}_{0}}^{3}}$ | D. | ($\frac{{R}_{M}+H}{{R}_{0}}$)3 |
分析 一个天体绕另一个天体做匀速圆周运动时,所需向心力由中心天体的万有引力提供,由牛顿第二定律列方程,求出天体质量的表达式,然后求出月球与地球的质量之比.
解答 解:设卫星质量是m,月球和地球的质量分别为M月和M地.卫星绕月球做圆周运动,由月球的万有引力提供卫星的向心力,由牛顿第二定律可得:
G$\frac{{M}_{月}m}{({R}_{M}+H)^{2}}=m\frac{4{π}^{2}}{{{T}_{M}}^{2}}$(RM+H),
月球质量:M月=$\frac{4{π}^{2}({R}_{M}+H)^{3}}{G{{T}_{M}}^{2}}$
同理,月球绕地球做圆周运动的向心力由地球对月球的万有引力提供,则由牛顿第二定律得:
G$\frac{{M}_{月}{M}_{地}}{{{R}_{0}}^{2}}={M}_{月}\frac{4{π}^{2}}{{{T}_{E}}^{2}}$R0,
地球质量:M地=$\frac{4{π}^{2}{{R}_{0}}^{3}}{G{{T}_{E}}^{2}}$,
所以:$\frac{{M}_{月}}{{M}_{地}}$=($\frac{{T}_{E}}{{T}_{M}}$)2•($\frac{{R}_{M}+H}{{R}_{0}}$)3,故A正确.
故选:A
点评 知道环绕天体的轨道半径和周期,可以求中心天体的质量,是常见的题型,关键要建立卫星运动的模型,明确万有引力提供卫星的向心力这一基本思路.

练习册系列答案
相关题目
4.下列关于电磁波的说法正确的是( )
| A. | 雷达使用X光来确定物体位置的设备 | |
| B. | 电磁波既可能是横波,也可能是纵波 | |
| C. | 均匀变化的电场可以产生恒定的磁场 | |
| D. | 用红外线照射时,大额钞票上用荧光物质印刷的文字会发出可见光 |
11.如图所示,小铁球在光滑水平面上一速度v做直线运动,当它经过磁铁附近后的运动轨迹可能是( )
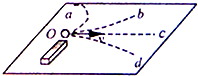

| A. | Od | B. | Oc | C. | Ob | D. | Oa |
8.入射光照到某金属表面上发生光电效应,若入射光的强度减弱,而频率保持不变,下列说法正确的是( )
| A. | 逸出的光电子的最大初动能减少 | |
| B. | 逸出的光电子的最大初动能不变 | |
| C. | 单位时间里从金属表面逸出的光电子数目减少 | |
| D. | 不发生光电效应 |
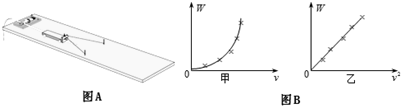
 一次执行特殊任务的过程中,飞行员在距地面320m高的水平面上做匀加速直线运动的某波音轻型飞机上依次抛出a、b、c三个物体,抛出的时间间隔为1s,抛出点a、b与b、c间距分别为45m和55m,三个物体分别落在水平地面上的A、B、C三处.求:
一次执行特殊任务的过程中,飞行员在距地面320m高的水平面上做匀加速直线运动的某波音轻型飞机上依次抛出a、b、c三个物体,抛出的时间间隔为1s,抛出点a、b与b、c间距分别为45m和55m,三个物体分别落在水平地面上的A、B、C三处.求: 如图所示,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$圆弧轨道,两轨道相切于B点.在外力作用下,小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力.已知小球刚好能沿圆轨道经过最高点C,重力加速度为g.求:
如图所示,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$圆弧轨道,两轨道相切于B点.在外力作用下,小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力.已知小球刚好能沿圆轨道经过最高点C,重力加速度为g.求: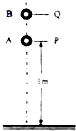 如图所示,从距水平地面高度h=1m的P点将小球A以大小为v0=4m/s的速度竖直向下抛出,在球A与地面碰后刚要离开地面时,将质量为m=2kg的小球B在P点正上方的Q点由静止释放,两球刚好在P点相碰,碰后B球恰好回到Q点,忽略空气阻力、碰撞时间及碰撞中的动能损失,取重力加速度g=10m/s2.
如图所示,从距水平地面高度h=1m的P点将小球A以大小为v0=4m/s的速度竖直向下抛出,在球A与地面碰后刚要离开地面时,将质量为m=2kg的小球B在P点正上方的Q点由静止释放,两球刚好在P点相碰,碰后B球恰好回到Q点,忽略空气阻力、碰撞时间及碰撞中的动能损失,取重力加速度g=10m/s2.