题目内容
如图8-7-4所示,在光滑的水平面上有一长l=2 m的木板C,在它的两端各有一块挡板.C的质量mc=5 kg,在C的中央,并排放着两个可视为质点的滑块A和B,mA=1 kg,mB=4 kg.开始时A、B、C均处于静止状态,并且A、B间夹有少量炸药,炸药爆炸使得A以vA=6 m/s的速度水平向左滑动.如果A、B与C间的摩擦可忽略不计(爆炸后A、B质量不变),两滑块中任一块与挡板碰撞后和挡板黏在一起,爆炸和碰撞的时间都可忽略.求: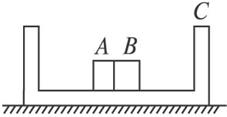
图8-7-4
(1)当两个滑块都与挡板黏在一起后,板C的速度是多大?
(2)从爆炸开始到两个滑块都与挡板碰撞为止,板C的位移是多大?方向如何?
解析:炸药爆炸的过程中A、B组成的系统动量守恒.当A或B或C碰撞时动量也守恒,从爆炸到A、B都与C黏在一起的过程中系统的总动量也守恒.
爆炸以后,由于A、B的质量不一样,因此他们的速率就不一样,他们与C相碰的先后次序就不一样,存在时间差.
(1)以A、B、C为研究对象,从爆炸开始到A、B、C合而为一,整个过程中系统不受外力作用,系统的动量守恒,故初动量为零,所以末动量也必然为零,所以板C在终态的速度vC=0.
(2)为了求板C的位置,先求爆炸后B的速度,因爆炸过程中A、B的动量守恒,以A的运动方向(向左)为正,则mAvA-mBvB=0.
已知vA=6 m/s,解得vB=![]() ×6 m/s=1.5 m/s(向右).由于vA>vB,开始时A、B又居C板的中央,所以A先与C相碰,再经过一段时间Δt,B才会与C相碰.
×6 m/s=1.5 m/s(向右).由于vA>vB,开始时A、B又居C板的中央,所以A先与C相碰,再经过一段时间Δt,B才会与C相碰.
以A和C为对象,设A与C相碰后共同速度为v,由动量守恒定律得:
mAvA=(mA+mC)v
解得v=![]() =1 m/s.
=1 m/s.
设从爆炸至A与C相碰历时t1,在A与C相碰时,B与C板右端相距为x,由运动学关系有
t1=![]() ,x=
,x=![]() -vBt1=
-vBt1=![]() -
-![]() =1 m-
=1 m-![]() m=0.75 m.
m=0.75 m.
A、C相碰后整体速度v=1 m/s(向左),再经Δt时间B又与C相碰.
以C为参考系,则有Δt=![]() =0.3 s.在这段时间内C板的位移为s=vΔt=1×0.3 m=0.3 m,方向向左.
=0.3 s.在这段时间内C板的位移为s=vΔt=1×0.3 m=0.3 m,方向向左.
答案:(1)0 (2)0.3 m 向左

练习册系列答案
相关题目