题目内容
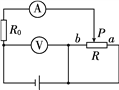
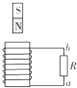
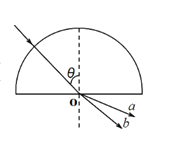
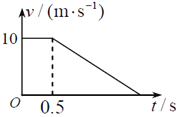
【题目】如图所示，一个“U”形金属导轨靠绝缘的墙壁水平放置，导轨长L=1.4m，宽d=0.2m．一对长L1=0.4m的等宽金属导轨靠墙倾斜放置，与水平导轨成θ角平滑连接，θ角可在0～60°调节后固定．水平导轨的左端长L2=0.4m的平面区域内有匀强磁场，方向水平向左，磁感应强度大小B0=2T．水平导轨的右端长L3=0.5m的区域有竖直向下的匀强磁场B，磁感应强度大小随时间以 
=1.0T/s均匀变大．一根质量m=0.04kg的金属杆MN从斜轨的最上端静止释放，金属杆与斜轨间的动摩擦因数1=0.125，与水平导轨间的动摩擦因数2=0.5．金属杆电阻R=0.08Ω，导轨电阻不计．
（1）求金属杆MN上的电流大小，并判断方向；
（2）金属杆MN从斜轨滑下后停在水平导轨上，求θ角多大时金属杆所停位置与墙面的距离最大，并求此最大距离xm ．
【答案】
（1）解：由法拉第电磁感应定律，则有：E= 
= 
dL3
由闭合电路欧姆定律得：I= 
由上式，可得MN棒上的电流大小：I=1.25A
根据右手定则，则MN棒上的电流方向：N→M
答：金属杆MN上的电流大小1.25A，且方向N→M
（2）解：设导体棒滑出水平磁场后继续滑行x后停下，
由动能定理得：mgL1sinθ﹣μ1mgL1cosθ﹣μ2（mg+B0Id）（L2﹣L1cosθ）﹣μ2mgx=0
代入数据得：
0.16sinθ+0.16cosθ﹣0.18=0.2x
当θ=45°时，x最大，
解得：x=0.8 
﹣0.9=0.23m
则有：xm=L2+x=0.63m
答：金属杆MN从斜轨滑下后停在水平导轨上，则夹角45°时金属杆所停位置与墙面的距离最大，
且最大距离0.63m．
【解析】（1）根据法拉第电磁感应定律，求得感应电动势大小，再依据闭合电路欧姆定律，求得感应电流的大小，最后根据右手定则，来判定感应电流的方向；（2）根据动能定理，列出表达式，再依据数据知识，当夹角θ取何值时，滑行位移有最大值，从而即可求解．
【考点精析】掌握动能定理的综合应用是解答本题的根本，需要知道应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
