题目内容
(18分)如图,水平地面上,质量为4m的凹槽被一特殊装置锁定处于静止状态,凹槽内质量为m的小木块压缩轻质弹簧后用细线固定(弹簧与小木块不粘连),此时小木块距离凹槽右侧为x;现细线被烧断,木块被弹簧弹出后与凹槽碰撞并粘连,同时装置锁定解除;此后木块与凹槽一起向右运动,测得凹槽在地面上移动的距离为s;设凹槽与地面的动摩擦因数为μ1,凹槽内表面与木块的动摩擦因数为µ2,重力加速度为g,求: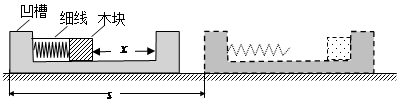
(1)木块与凹槽碰撞后瞬间的共同速度大小v;
(2)细线被烧断前弹簧储存的弹性势能。
(1)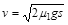 (2)
(2)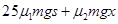
解析试题分析:(1)设木块与凹槽碰撞后共同速度为v,由动能定理: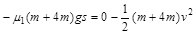 (3分)
(3分)
可得: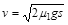 (3分)
(3分)
(2)设木块与凹槽碰撞前瞬间的速度为v1,由动量守恒: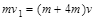 (3分)
(3分)
可得: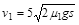 (3分)
(3分)
木块被弹开到与凹槽碰撞,由动能定理,有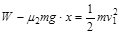 (3分)
(3分)
可得 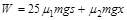 (2分)
(2分)
由功能关系,细线被烧断前弹簧储存的弹性势能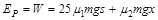 (1分)
(1分)
考点:本题考查动能定理和动量守恒定律。

练习册系列答案
相关题目
探究能力是物理学研究的重要能力之一,物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关,为了研究砂轮的转动动能Ek与角速度ω的关系,某同学采用了下述实验方法进行探究:先让砂轮由动力带动匀速旋转,测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据,得出结论。经实验测得的几组ω和n如下表所示:
| ω/rad?s-1 | 0.5 | 1 | 2 | 3 | 4 |
| n | 5.0 | 20 | 80 | 180 | 320 |
| Ek/J | | | | | |
另外已测得砂轮转轴的直径为1 cm,转轴间的摩擦力为

(1)计算出砂轮每次脱离动力的转动动能,并填入上表中。
(2)由上述数据推导出砂轮转动动能与角速度的关系式为________________。
 m/s沿AB方向从A点进入电场,恰好穿过孔O1和O2后,从H点离开电场。金属板间的距离L1=2 cm,L2=4 cm,L3=6 cm。电子质量
m/s沿AB方向从A点进入电场,恰好穿过孔O1和O2后,从H点离开电场。金属板间的距离L1=2 cm,L2=4 cm,L3=6 cm。电子质量 kg,电荷量
kg,电荷量 C。正对的两平行板间可视为匀强电场,求:
C。正对的两平行板间可视为匀强电场,求:



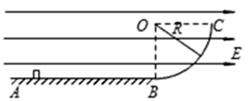
 的带正电的小球,为使小球刚好在圆轨道内做圆周运动,求释放点A距圆轨道最低点B的距离
的带正电的小球,为使小球刚好在圆轨道内做圆周运动,求释放点A距圆轨道最低点B的距离 .已知小球受到的电场力大小等于小球重力的
.已知小球受到的电场力大小等于小球重力的 倍.
倍. 
 。战机从A点开始滑跑,C点离舰,此过程中发动机的推力和飞机所受甲板和空气阻力的合力大小恒为F,ABC甲板总长度为L,战斗机质量为m,离舰时的速度为vm,不计飞机在B处的机械能损失。求AB部分的长度。
。战机从A点开始滑跑,C点离舰,此过程中发动机的推力和飞机所受甲板和空气阻力的合力大小恒为F,ABC甲板总长度为L,战斗机质量为m,离舰时的速度为vm,不计飞机在B处的机械能损失。求AB部分的长度。