题目内容
伞底圆半径R=0.6m，离地0.8m．当伞以 2r/s的转速转动时，水滴从伞边缘在水平方向沿切线飞出，则水滴从飞出点到着地点的水平距离为 m；水滴在地上洒开的圆周半径为 m．（取重力加速度g=10m/s2）
【答案】分析：水滴离开伞后做平抛运动，根据v=ωr求得线速度，即平抛运动的初速度，由平抛运动的规律可得出水滴从飞出点到着地点的水平距离，再结合几何关系即可求解水滴在地上洒开的圆周半径．
解答：解：根据v=ωR得：v=0.6×2=1.2m/s
水滴离开伞后做平抛运动，
h=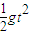
解得：t=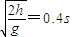
所以水平距离为x=vt=0.48m
雨滴运动的俯视图如图所示：
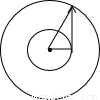
根据几何关系得：
r2=R2+s2
解得：r=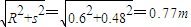
故答案为：0.48；0.77
点评：本题结合生活实际考查平抛运动的知识，通过画图找出水滴的水平位移为解题的关键，由高度即可求得时间，难度适中．
解答：解：根据v=ωR得：v=0.6×2=1.2m/s
水滴离开伞后做平抛运动，
h=
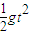
解得：t=
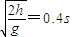
所以水平距离为x=vt=0.48m
雨滴运动的俯视图如图所示：
根据几何关系得：
r2=R2+s2
解得：r=
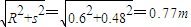
故答案为：0.48；0.77
点评：本题结合生活实际考查平抛运动的知识，通过画图找出水滴的水平位移为解题的关键，由高度即可求得时间，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
（2010?徐汇区一模）如图所示，半径R=0.6m的光滑半圆细环竖直放置并固定在水平桌面上，环上套有质量为1kg的小球甲，用一根细线将小球甲通过两个光滑定滑轮B、D与质量为2kg的小物体乙相连，滑轮的大小不计，与半圆环在同一竖直平面内，它们距离桌面的高度均为h=0.8m，滑轮B恰好在圆环最高点C点的正上方．初始时将甲拉至半圆环左边最低点A处，然后将甲、乙由静止开始释放，则当甲运动到离桌面高度为