题目内容
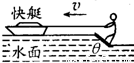
在电视节目中我们常常能看到一种精彩的水上运动——滑水板,如图5-12所示.运动员在快艇的水平牵引力作用下,脚踏倾斜滑板在水上匀速滑行,设滑板是光滑的.若运动员与滑板的总质量为m=70 kg,滑板的总面积为S=0.12 m2,水的密度为ρ=1.0×103 kg/m3.理论研究表明:当滑板与水平方向的夹角(板前端抬起的角度)为θ时,水对板的作用力大小为N=ρSv2sin2θ,方向垂直于板面.式中v为快艇的牵引速度,S为滑板的滑水面积,求为了使滑板能在水面上滑行,快艇水平牵引滑板的最小速度.
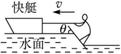
图5-12
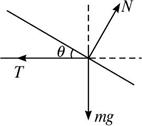
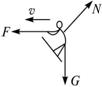
思路解析:从电视节目中可以看到,滑水运动员在快艇牵引下的滑行过程中,经常变换姿势,其实既是为使运动具有观赏性,也是出于平衡的需要.滑板与水平方向间的夹角θ与快艇的牵引速度v等都是互相联系的.要解决“快艇牵引滑板的最小速度”问题,首先需要弄清S、v、θ等物理量之间的相互关系.为此,选取滑板与运动员作为研究对象,对其作受力分析,滑板与运动员共受到三个力的作用:重力G、水对滑板的弹力N(方向与滑板板面垂直)及绳子对运动员的拉力F.为使问题简化,作为理想化处理,可不计水对滑板的阻力,受力图如图所示.由物体的平衡条件可得Ncosθ-mg=0.又由题中给出的理论模型N=ρSv2sin2θ
可得牵引速度为v=![]()
即在运动员与滑板的质量一定、滑板的总面积S一定时,维持滑板平衡所需的牵引速度大小仅由滑板与水平方向的夹角θ决定.或者说,快艇对运动员与滑板的牵引速度v是滑板倾角θ的函数.当θ取某一值时,牵引速度有最小值.下面我们就用求函数极值的方法来求解最小速度问题.
令k=sin2θcosθ,则有k2=![]() sin2θsin2θ(2cos2θ).
sin2θsin2θ(2cos2θ).
由数学中的基本不等式abc≤(![]() )3
)3
可得k2≤![]() (
(![]() )3=
)3=![]() ×(
×(![]() )3,当且仅当2cos2θ=sin2θ,
)3,当且仅当2cos2θ=sin2θ,
即θ=arctan![]() =54.7°时,k有最大值,即kmax=
=54.7°时,k有最大值,即kmax=![]()

 黄冈创优卷系列答案
黄冈创优卷系列答案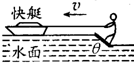 在电视节目中我们常常能看到一种精彩的水上运动--滑水板,如图所示.运动员在快艇的水平牵引力作用下,脚踏倾斜滑板在水上匀速滑行,设滑板是光滑的.若运动员与滑板的总质量为m=70kg,滑板的总面积为S=0.12m2,水的密度为ρ=1.0×103 kg/m3.理论研究表明:当滑板与水平方向的夹角(板前端抬起的角度)为θ时,水对板的作用力大小为N=ρSv2sin2θ,方向垂直于板面.式中v为快艇的牵引速度,S为滑板的滑水面积,求为了使滑板能在水面上滑行,快艇水平牵引滑板的最小速度.
在电视节目中我们常常能看到一种精彩的水上运动--滑水板,如图所示.运动员在快艇的水平牵引力作用下,脚踏倾斜滑板在水上匀速滑行,设滑板是光滑的.若运动员与滑板的总质量为m=70kg,滑板的总面积为S=0.12m2,水的密度为ρ=1.0×103 kg/m3.理论研究表明:当滑板与水平方向的夹角(板前端抬起的角度)为θ时,水对板的作用力大小为N=ρSv2sin2θ,方向垂直于板面.式中v为快艇的牵引速度,S为滑板的滑水面积,求为了使滑板能在水面上滑行,快艇水平牵引滑板的最小速度.