题目内容
 如图所示为一双线摆,它是由两根等长细绳悬挂一小球而构成的,绳的质量可以忽略.已知两绳长均为l,绳与水平方向夹角为α,当摆球A垂直于纸面做简谐运动经过平衡位置时,另一个小球B从A球的正上方开始做自由落体运动,且正好打在A球上,则小球B距平衡位置高度h可能为多少?
如图所示为一双线摆,它是由两根等长细绳悬挂一小球而构成的,绳的质量可以忽略.已知两绳长均为l,绳与水平方向夹角为α,当摆球A垂直于纸面做简谐运动经过平衡位置时,另一个小球B从A球的正上方开始做自由落体运动,且正好打在A球上,则小球B距平衡位置高度h可能为多少?某同学解法如下:
双线摆在摆动过程中周期T=2π
|
| T |
| 2 |
| T |
| 2 |
|
B球做自由落体:h=
| 1 |
| 2 |
且tA=tB (3)
解(1)、(2)、(3)式就可以求得h.
你认为上述分析是否正确?如果你认为正确,请完成此题;如果你认为不正确,请指出错误,并给出正确的解答.
分析:双线摆在摆动过程中,等效摆长l′=lsinα,周期T=2π
;
A球从平衡位置每经过
回到平衡位置均有可能与B球相碰;
再根据自由落体运动的位移公式计算,化简可得小球B距平衡位置高度h.
|
A球从平衡位置每经过
| T |
| 2 |
再根据自由落体运动的位移公式计算,化简可得小球B距平衡位置高度h.
解答:解:不正确.
此同学在解题过程中有两处错误:①双线摆在摆动过程中,等效摆长l′=lsinα,周期T=2π
②A球从平衡位置每经过
回到平衡位置均有可能与B球相碰,
则tA=
(k=1,2,3…)
又h=
gtB2,
且tA=tB
可得:h=
g(kπ
)2=
k2π2lsinα (k=1,2,3,…)
答:该同学的分析不正确,理由和正确分析如上所述,小球B距平衡位置高度h可能为
k2π2lsinα (k=1,2,3,…).
此同学在解题过程中有两处错误:①双线摆在摆动过程中,等效摆长l′=lsinα,周期T=2π
|
②A球从平衡位置每经过
| T |
| 2 |
则tA=
| kT |
| 2 |
又h=
| 1 |
| 2 |
且tA=tB
可得:h=
| 1 |
| 2 |
|
| 1 |
| 2 |
答:该同学的分析不正确,理由和正确分析如上所述,小球B距平衡位置高度h可能为
| 1 |
| 2 |
点评:本题要知道双线摆的摆长不是球心到悬点的距离,而是球心到等效悬点的距离,这一点是解题的关键.

练习册系列答案
相关题目

 如图所示为一双线摆,它是在一天花板上用两根等长的细线悬挂一小球而构成的,图中α和L均已知,当小球在垂直于纸面的平面内作简谐振动时,其周期为多少
如图所示为一双线摆,它是在一天花板上用两根等长的细线悬挂一小球而构成的,图中α和L均已知,当小球在垂直于纸面的平面内作简谐振动时,其周期为多少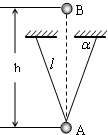
 ,A球从平衡位置经过
,A球从平衡位置经过 再次回到平衡位置时与B球相碰则tA=
再次回到平衡位置时与B球相碰则tA= =π
=π (1)
(1) gtB2 (2);
gtB2 (2); 