题目内容
11.如图1,在真空中足够大的绝缘水平地面上,一个质量为m=0.2kg,带电量为q=+2.0×10-6C的小物块处于静止状态,小物块与地面间的动摩擦因数μ=0.1.从t=0时刻开始,空间加上一个如图2所示的场强大小和方向是周期性变化的电场.(取水平向右的方向为正方向,g取10m/s2)求: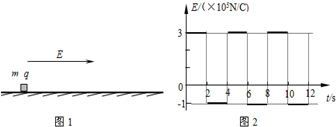
(1)物块在前2s内加速度的大小;
(2)物块在前4s内的位移大小;
(3)23秒内电场力对小物块所做的功.
分析 (1)小物块在水平地面上受电场力和摩擦力,由牛顿第二定律求出加速度,然后由速度公式求出速度;
(2)根据物体的受力判断物体的运动,根据运动学公式求出物体位移.
(3)根据动能定理求电场力对小物块所做的功.
解答 解:(1)根据牛顿第二定律解得:
0~2s内物块加速度:a1=$\frac{q{E}_{1}-μmg}{m}$=2m/s2,
2s末物块的速度:v1=a1t1=2×2=4m/s;
(2)2~4s内物块做匀减速运动,加速度大小:a2=$\frac{q{E}_{2}+μmg}{m}$=2m/s2,
0~2s内物块的位移为:s1=$\frac{1}{2}$a1t12=4m,
2~4s内的位移为:s2=v1t2-$\frac{1}{2}$a2t22=4m,
4秒内小物块的位移大小为:x=s1+s2=4+4m=8m;
(3)4s末的速度为v4=0
则小物块做周期为4s的匀加速和匀减速运动.
第22s末小物块的速度为v=4m/s,前22s内位移为S22=$\frac{22}{2}{S}_{1}$=44m
第23s内物块的位移为S23=vt+$\frac{1}{2}{a}_{2}{t}^{2}$,t=1s,S23=3m
故23秒内小物块的位移大小为47m.
物块在第23s末的速度为v23=2m/s.
根据动能定理得
W-μmgS23=$\frac{1}{2}m{v}_{23}^{2}$
代入解得 W=9.8J.
答:(1)2秒末小物块的速度大小为4m/s;
(2)4秒内小物块的位移大小为8m;
(3)23秒内电场力对小物块所做的功为9.8J.
点评 解决本题的关键能够正确地进行受力分析,通过物体的受力,判断物体的运动,结合牛顿第二定律和运动学公式和动能定理进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.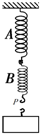 如图所示,两劲度系数分别为k1和k2的轻质弹簧A、B串接在一起后竖直悬挂起来,然后将一个重为G的钩码挂在B下端,待整个系统平衡时,B下端的挂钩P下降的高度为( )
如图所示,两劲度系数分别为k1和k2的轻质弹簧A、B串接在一起后竖直悬挂起来,然后将一个重为G的钩码挂在B下端,待整个系统平衡时,B下端的挂钩P下降的高度为( )
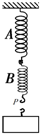 如图所示,两劲度系数分别为k1和k2的轻质弹簧A、B串接在一起后竖直悬挂起来,然后将一个重为G的钩码挂在B下端,待整个系统平衡时,B下端的挂钩P下降的高度为( )
如图所示,两劲度系数分别为k1和k2的轻质弹簧A、B串接在一起后竖直悬挂起来,然后将一个重为G的钩码挂在B下端,待整个系统平衡时,B下端的挂钩P下降的高度为( )| A. | $\frac{G}{{k}_{1}+{k}_{2}}$ | B. | $\frac{G{k}_{1}{k}_{2}}{{k}_{1}+{k}_{2}}$ | C. | $\frac{G({k}_{1}+{k}_{2})}{{k}_{1}{k}_{2}}$ | D. | $\frac{G}{{k}_{2}}$ |
19.如图所示电路,电源电压不变,闭合开关,当滑动变阻器滑片P向左滑动时,出现的现象是( )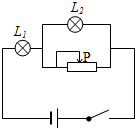

| A. | L1变暗,L2变暗 | B. | L1变暗,L2变亮 | C. | L1变亮,L2变暗 | D. | L1变亮,L2变亮 |
16.甲、乙两同学沿同一方向,水平向右拉一木箱,甲用60N的力,乙用40N的力,木箱在水平地面上做匀速运动,则木箱受到地面的滑动摩擦力的大小和方向分别是( )
| A. | 100N,方向向右 | B. | 100N,方向向左 | C. | 20N,方向向右 | D. | 20N,方向向左 |
20.做匀变速直线运动的物体位移随时间的变化规律为s=18t-1.5t2(m),根据这一关系式可以知道( )
| A. | t=12s时物体的速度为零 | |
| B. | t=6s时物体的速度为零 | |
| C. | t=12s时物体运动回原位置 | |
| D. | t=12s时物体的速度和位移都发生改变 |
1.一小车从静止出发从A地运动到B地,先做匀加速直线运动,然后保持匀速运动最后匀减速运动直到停止,从开始运动起计时,下表为小车某些时刻的瞬时速度,根据表中数据可知( )
| 时刻(s) | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5 |
| 速度(m/s) | 3.0 | 6.0 | 9.0 | 12 | 12 | 9.0 | 3.0 |
| A. | 小车加速运动的时间为5s | B. | 小车匀速运动的时间为5s | ||
| C. | 小车减速运动的时间为2s | D. | 小车运动的总位移为96m |
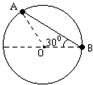 一光滑圆环固定在竖直平面内,环上套着两个小球A和B(中央有孔),A、B间由细绳连接着,它们处于如图所示位置时恰好都能保持静止状态.此情况下,B球与环中心O处于同一水平面上,AB间的细绳呈伸直状态,与水平线成30°夹角.已知B球的质量为m,求:
一光滑圆环固定在竖直平面内,环上套着两个小球A和B(中央有孔),A、B间由细绳连接着,它们处于如图所示位置时恰好都能保持静止状态.此情况下,B球与环中心O处于同一水平面上,AB间的细绳呈伸直状态,与水平线成30°夹角.已知B球的质量为m,求:
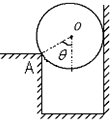 如图所示,一个质量为10Kg的小球被夹在竖直的墙壁和A点之间,已知球心O与A点的连线与竖直方向成θ角,且θ=37°,所有接触点和面均不计摩擦.(g=10N/Kg,sin37°=0.6;cos37°=0.8;tan37°=0.75)
如图所示,一个质量为10Kg的小球被夹在竖直的墙壁和A点之间,已知球心O与A点的连线与竖直方向成θ角,且θ=37°,所有接触点和面均不计摩擦.(g=10N/Kg,sin37°=0.6;cos37°=0.8;tan37°=0.75)