题目内容
 如图所示,细绳OA水平,细绳OB与水平方向成37°夹角,悬挂物体M处于静止状态,设细绳OA、OB所承受的最大拉力大小分别为F1=50N、F2=100N,OC细绳不会断,则
如图所示,细绳OA水平,细绳OB与水平方向成37°夹角,悬挂物体M处于静止状态,设细绳OA、OB所承受的最大拉力大小分别为F1=50N、F2=100N,OC细绳不会断,则(1)随着所挂重物重量的增加,哪根绳先断,为什么?
(2)最重可以挂多重的物体?(sin37°=0.6,cos37°=0.8,g=10m/s2)
分析:(1)对结点受力分析,运用假设法,假设某一根绳子先断,根据共点力平衡求出求出另一根绳子的拉力,判断是否大于它的最大拉力,从而判断出哪个绳子先断.
(2)根据先断的那个绳的最大拉力,根据共点力平衡求出悬挂重物的最大重力.
(2)根据先断的那个绳的最大拉力,根据共点力平衡求出悬挂重物的最大重力.
解答:解: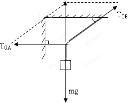 (1)假设AO绳先达到最大拉力,则F1=50N.
(1)假设AO绳先达到最大拉力,则F1=50N.
cos37°=
,解得F2=
=
N=62.5N<100N
可知AO绳先断.
(2)因为AO绳先达到最大拉力,知F1=50N
则tan37°=
.
所以G=F1tan37°=50×
N=37.5N.
答:(1)随着所挂重物重量的增加,AO绳先断.
(2)最重可以挂37.5N的重物.
 (1)假设AO绳先达到最大拉力,则F1=50N.
(1)假设AO绳先达到最大拉力,则F1=50N.cos37°=
| F1 |
| F2 |
| F1 |
| cos37° |
| 50 |
| 0.8 |
可知AO绳先断.
(2)因为AO绳先达到最大拉力,知F1=50N
则tan37°=
| G |
| F1 |
所以G=F1tan37°=50×
| 3 |
| 4 |
答:(1)随着所挂重物重量的增加,AO绳先断.
(2)最重可以挂37.5N的重物.
点评:解决本题的关键能够正确地进行受力分析,运用共点力平衡进行求解.本题采用假设法比较简单,方便.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 的公式为
的公式为
