题目内容
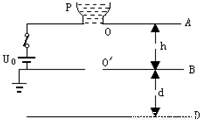
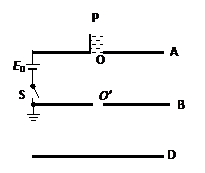
三块相同的金属平板A、B、D自上而下水平放置,间距分别为h和d,如图所示。A、B两板中心开孔,在A板的开孔上搁有一金属容器P,与A板接触良好,其内盛有导电液体。A板通过闭合的开关S与电动势为E0的电池的正极相连,B板与电池的负极相连并接地。容器P内的液体在在底部小孔O处形成质量为m、带电量为q的液滴后自由下落,穿过B板的开孔![]() 落在D板上,其电荷被D板吸收,液体随即蒸发,接着容器底部又形成相同的液滴自由下落,如此继续,设整个装置放在真空中。
落在D板上,其电荷被D板吸收,液体随即蒸发,接着容器底部又形成相同的液滴自由下落,如此继续,设整个装置放在真空中。
(1)第一个液滴到达D板时的速度为多少?
(2)D板最终可达到多高的电势?
(3)设液滴的电荷量是A板所带电量的α倍(α=0.02),A板与B板构成的电容器的电容为C0=5×10-12F,E0=1000V,m=0.02g,h=d=5cm。试计算D板最终的电势值。(g=10m/s2)
(4)如果开关S不是始终闭合,而只是在第一个液滴形成前闭合一下,随即打开,其它条件与(3)相同。在这种情况下,设想第n滴液滴能落至D板,则当第n滴液滴刚刚下落的时刻,D板的电势多高?D板最终可达到多高的电势?
(1)![]() (2)
(2)![]() (3)1000V
(3)1000V
解析:
(1)设第一个液滴到达D板时的速度为v,由动能定理
![]() ①
①
得 ![]() ②
②
(2)当D板电势为![]() 时,液滴到达D板的动能为
时,液滴到达D板的动能为
![]() ③
③
令![]() 得
得 ![]() ④
④
(3)![]() ⑤
⑤
(4)D板的电势主要取决于D板的带电量,当第(n-1)滴液滴落至D板后,D板的带电量为(A板总电量减去A板剩余电量)
![]() ⑥
⑥
故当第n滴液滴刚刚下落的时刻,D板的电势为
![]() V ⑦
V ⑦
显然当n→∞时,![]() V,即D板最终的电势为1000V。
V,即D板最终的电势为1000V。
但是这里的问题是,是不是所有的液滴都能到达D板,这里必须进行鉴定。由于D板电势最高不能超过1000V,所有的液滴的电量都不超过![]() (即第一滴液滴的电量),若电量为
(即第一滴液滴的电量),若电量为![]() 的液滴在D板电势为1000V时都能到达D板,那么其它的液滴(即所有的液滴)必定能到达D板。对这样的情形,根据动能定理
的液滴在D板电势为1000V时都能到达D板,那么其它的液滴(即所有的液滴)必定能到达D板。对这样的情形,根据动能定理
![]()
代入数据,显然有![]() ⑧
⑧
这说明液滴可以一直滴下去,直至A板上所有的电荷都转移到D板,即D板最终的电势可达1000V。

 口算题天天练系列答案
口算题天天练系列答案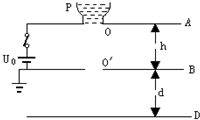 三块相同的金属平板A、B、D自上而下水平放置,间距分别为h和d,如图所示.A、B两板中心开孔,在A板的开孔上搁有一金属容器P,与A板接触良好,其内盛有导电液体.A板通过闭合的电键K与电动势为U0的电池正极相连,B板与电池负极相连并接地.容器P内液体在底部小孔O处形成质量为m,带电量为q的液滴后自由下落,穿过B板的开孔O′落到D板上,其电荷被D板吸附,液体随即蒸发.接着容器底部又形成相同的液滴自由下落,如此继续.设整个装置放在真空中.
三块相同的金属平板A、B、D自上而下水平放置,间距分别为h和d,如图所示.A、B两板中心开孔,在A板的开孔上搁有一金属容器P,与A板接触良好,其内盛有导电液体.A板通过闭合的电键K与电动势为U0的电池正极相连,B板与电池负极相连并接地.容器P内液体在底部小孔O处形成质量为m,带电量为q的液滴后自由下落,穿过B板的开孔O′落到D板上,其电荷被D板吸附,液体随即蒸发.接着容器底部又形成相同的液滴自由下落,如此继续.设整个装置放在真空中.