题目内容
16.近地人造卫星1和2绕地球做匀速圆周运动的周期分别为T1和T2,设在卫星1、卫星2各自所在的高度上的重力加速度大小分别为g1、g2,则( )| A. | $\frac{{g}_{1}}{{g}_{2}}$=($\frac{{T}_{1}}{{T}_{2}}$)${\;}^{\frac{3}{4}}$ | B. | $\frac{{g}_{1}}{{g}_{2}}$=($\frac{{T}_{2}}{{T}_{1}}$)${\;}^{\frac{4}{3}}$ | ||
| C. | $\frac{{g}_{1}}{{g}_{2}}$=($\frac{{T}_{1}}{{T}_{2}}$)2 | D. | $\frac{{g}_{1}}{{g}_{2}}$=($\frac{{T}_{2}}{{T}_{1}}$)2 |
分析 要求重力加速度g之比,必须求出重力加速度g的表达式,而g与卫星的轨道半径r有关,根据已知条件需要求出r和卫星的运动周期之间的关系式
解答 解:人造卫星在地球的引力的作用下绕地球做圆周运动,则有
G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r
忽略地球的自转,则有
mg=G$\frac{Mm}{{r}^{2}}$
解得g=GM$(\frac{4{π}^{2}}{GM{T}^{2}})^{\frac{2}{3}}$
故$\frac{{g}_{1}}{{g}_{2}}=(\frac{{T}_{2}}{{T}_{1}})^{\frac{4}{3}}$
故选:B
点评 这类题目在万有引力与航天中比较常见,本题反映了这类题目常规的解题思路和方法,需要我们认真理解和领会

练习册系列答案
相关题目
4.做下列运动的物体,能当做质点处理的是( )
| A. | 自转中的地球 | |
| B. | 裁判员眼中的3米板跳台跳水的运动员 | |
| C. | 匀速直线运动的火车 | |
| D. | 旋转中的风力发电机的叶片 |
11.下列说法中正确的是( )
| A. | 运动物体所受的合外力不为零,物体的动能一定要变化 | |
| B. | 动能不变的物体,一定处于平衡状态 | |
| C. | 只要重力做功,重力势能一定改变 | |
| D. | 力对物体做功越大,力的功率一定越大 |
1.以下说法正确的是( )
| A. | 磁铁吸引铁钉,是因为磁铁对铁钉施加了力的作用,而铁钉没有对磁铁施力 | |
| B. | 书对桌面施加了压力,是因为书发生了形变 | |
| C. | 同一物体在地球上不同地方所受重力都相同 | |
| D. | 滑动摩擦力的方向总是与物体运动方向相反 |
5.设电子在运动过程中只受电场力作用.在下述的哪一种电场中可能出现以下情况:只要给电子一个适当的初速度它就能始终沿同一条电场线运动;而给电子另一个适当的初速度它就能始终沿某一个等势面运动( )
| A. | 正点电荷产生的电场 | B. | 负点电荷产生的电场 | ||
| C. | 等量同种点电荷产生的电场 | D. | 等量异种点电荷产生的电场 |
6.如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力和运动情况是( )
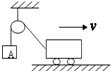

| A. | 绳的拉力大于A的重力 | B. | 绳的拉力等于A的重力 | ||
| C. | 绳的拉力小于A的重力 | D. | 物体A的速度会逐渐增大 |
 如图所示,水平面上有两个物体A和B,质量均为m,A以角速度w绕半径为R的圆做逆时针匀速圆周运动.当它经过P点时,物体B在恒力F作用下开始运动,F的方向与A物体在P点时刻的速度方向垂直.当F满足什么条件时,两物体在运动过程中的某时刻会具有相同的动量.
如图所示,水平面上有两个物体A和B,质量均为m,A以角速度w绕半径为R的圆做逆时针匀速圆周运动.当它经过P点时,物体B在恒力F作用下开始运动,F的方向与A物体在P点时刻的速度方向垂直.当F满足什么条件时,两物体在运动过程中的某时刻会具有相同的动量.