题目内容
如图12所示，平行板电容器两极板水平放置，当电容器带电荷量为Q时在两板内a处有一带电荷量为q的油滴恰能保持静止状态.现让电容器放出Q／2电荷，油滴将向下竖直加速，经过时间t到达b点.为使油滴从b点开始，经过相同的时间t（假如油滴不会撞在B板上）能返回到a处，则当油滴抵达b处时，需再给电容器充多少电?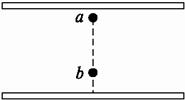
图12
2Q
解析：设原来电荷量为Q时，两极板间的场强为E0，则对油滴有G=qE0，放出Q／2电荷后场强变为E0/2，油滴的加速度a1=(G- qE0/2)/m=g/2.从a到b有s=a1t2/2；从b到a有：-s=a1t2-a2t2/2，所以a2=
练习册系列答案
名校课堂系列答案
相关题目
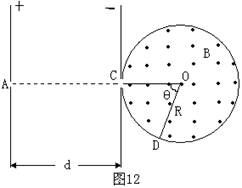（06年广东卷）（17 分）在光滑绝缘的水平桌面上，有两个质量均为m，电量为＋q的完全相同的带电粒子P1和P2，在小孔A处以初速度为零先后释放。在平行板间距为d的匀强电场中加速后，P1从C处对着圆心进入半径为R的固定圆筒中（筒壁上的小孔C只能容一个粒子通过），圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场。P1每次与筒壁发生碰撞均无电荷迁移，P1进入磁场第一次与筒壁碰撞点为D，∠COD=θ，如图12所示。延后释放的P2，将第一次欲逃逸出圆筒的P1正碰圆筒内，此次碰撞刚结束，立即改变平行板间的电压，并利用P2与P1之后的碰撞，将P1限制在圆筒内运动。碰撞过程均无机械能损失。设d=
，求：在P2和P1相邻两次碰撞时间间隔内，粒子P1与筒壁的可能碰撞次数。
附：部分三角函数值
|
|
|
|
|
|
|
|
|
|
tan | 3.08 | 1.37 | 1.00 | 0.73 | 0.58 | 0.48 | 0.41 | 0.36 | 0.32 |
.