��Ŀ����
����Ŀ�������ڹ۲��������������Ѿ������ˡ�˫��ϵͳ������˫��ϵͳ�����������Ͻ��ĺ�����ɣ�ÿ�����ǵ��߶�ԶС����������֮��ľ��룬����˫��ϵͳһ��Զ���������壮��ͼ������������ɵ�˫�ǣ����֮����������������£��������ϵ�O��������Բ���˶����ֲ��������֮��ľ���ΪL������֮��Ϊm1��m2=3��2�����֪�� ��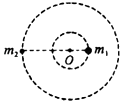
A.m1��m2��Բ���˶��Ľ��ٶ�֮��Ϊ2��3
B.m1��m2��Բ���˶������ٶ�֮��Ϊ3��2
C.m1��Բ���˶��İ뾶Ϊ ![]()
D.m1��m2��Բ���˶�����������С���
���𰸡�C,D
���������⣺˫��Χ�������ϵ�O��������Բ���˶����˴˼����������ṩԲ���˶�����������֪˫����Բ���˶������ںͽ��ٶ���ȣ�����m1�İ뾶Ϊr������m2�İ뾶Ϊl��r
����
�����������ṩԲ���˶��������У�G ![]() =m1r��2=m2��l��r����2
=m1r��2=m2��l��r����2
��m1r=m2��l��r��
�� ![]() =3��2
=3��2
�������r= ![]() L
L
����m2�İ뾶Ϊ ![]() L����A����C��ȷ��D��ȷ
L����A����C��ȷ��D��ȷ
B������Ϊv=r�ؿ�֪��������Բ���˶������ٶ�֮�ȵ��ڰ뾶֮�ȼ��� ![]() =
= ![]() ����B����
����B����
��ѡ��CD��
ץס˫��Χ�������ϵ�O��������Բ���˶����������ɱ˴˼�����������ṩ�����������Բ���˶��Ľ��ٶ���ȣ��ɴ�չ�����ۼ��ɣ�