题目内容
物体做直线运动的位移s与时间t的关系为s =" 5t+" t 2，则该物体
| A．物体运动的初速度是5m/s |
| B．物体运动的加速度是1m/s2 |
| C．第1s内的位移是5m |
| D．任意相邻1s内的位移差都是1m |
A
解析试题分析：物体做直线运动的位移s与时间t的关系为s =" 5t+" t 2，与位移与时间的关系s=v0t+
at2做对比，可得出物体运动的初速度为5m/s，故A是正确的；物体运动的加速度是2m/s2，故B不对；
将t=1s代入关系式中，就可以得出第1s内的位移是6m，故C不对；利用公式△s=at2，可得任意相邻1s内的位移差都是2m，故D是不对的。
考点：匀变速直线运动中的位移与时间的关系式。
如图所示，小球以一定初速度沿粗糙斜面向上做匀减速直线运动，依次经a、b、c、d 到达最高点e。已知ab="bd=6" m，bc="1" m，小球从a到c和从c到d所用时间都是2 s。设小球经b、c时的速度分别为vb、vc，则 
A．vb=  m/s | B． m/s |
| C．de="3" m | D．从d到e所用时间为4 s |
如图，穿在水平直杆上质量为m的小球开始时静止.现对小球沿杆方向施加恒力F0，垂直于杆方向施加竖直向上的力F，且F的大小始终与小球的速度成正比，即F=kυ（图中未标出）.已知小球与杆间的动摩擦因数为μ，已知小球运动过程中未从杆上脱落，球上小孔直径略大于直杆直径，且F0>μmg.下列说法正确的是：（ ） 
| A．小球先做加速度减小的加速运动，后做加速度增大的减速运动直到静止 |
| B．小球先做加速度增大的加速运动，后做加速度减小的加速运动，直到最后做匀速运动 |
C．小球的最大加速度为 |
D．恒力F0的最大功率为 |
一物体做匀减速运动，一段时间△t（未知）内通过的位移为x1，紧接着△t时间内通过的位移为x2，又紧接着经过位移x（未知）物体的速度减小为0，则
| A．可求△t | B．可求加速度a的大小 |
| C．△t和加速度a 的大小均不可求 | D．可求x，x＝ |
如图所示，一个楔形物体M放在固定的粗糙斜面上，M上表面水平且光滑，下表面粗糙，在其上表面上放一光滑小球m，楔形物体由静止释放，则小球在碰到斜面前的运动轨迹是 ( )
| A．沿斜面方向的直线 | B．竖直向下的直线 |
| C．无规则的曲线 | D．抛物线 |
如图甲所示，为测定物体冲上粗糙斜面能达到的最大位移x与斜面倾角
的关系，将某一物体每次以不变的初速率
沿足够长的斜面向上推出，调节斜面与水平方向的夹角，实验测得x与斜面倾角的关系如图乙所示，g取
，根据图象可求出
| A．物体的初速率=3m／s |
B．物体与斜面间的动摩擦因数 |
C．取不同的倾角，物体在斜面上能达到的位移x的最小值 |
D．当某次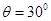 时，物体达到最大位移后将沿斜面下滑 |
汽车遇紧急情况刹车，经1.5 s停止，刹车距离为9 m.若汽车刹车后做匀减速直线运动，则汽车停止前最后1 s的位移是( )
| A．4.5 m | B．4 m | C．3 m | D．2 m |
利用传感器和计算机可以研究快速变化的力的大小， 实验时让质量为M的某消防员从一平台上自由下落，落地过程中先双脚触地，接着他用双腿弯曲的方法缓冲，使自身重心又下降了段距离，最后停止，用这种方法获得消防员受到地面冲击力随时间变化的图线如图所示。 根据图线所提供的信息，以下判断正确的是( ) 
| A．t1时刻消防员的速度最大 |
| B．t2时刻消防员的速度最大 |
| C．t3时刻消防员的速度最大 |
| D．t4时刻消防员的速度最大 |
“星跳水立方”节目中，某明星从跳板处由静止往下跳的过程中(运动过程中某明星可视为质点)，其速度—时间图象如图所示，则下列说法正确的是( )．
| A．跳板距离水面的高度为10 m |
| B．该明星入水前处于失重状态，入水后处于超重状态 |
| C．1 s末该明星的速度方向发生改变 |
| D．该明星在整个下跳过程中的平均速度是5 m/s |