题目内容
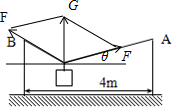
 如图所示,长为5m的细绳两端分别系于竖立在地面上相距为4m的两杆的顶端A、B.绳上挂一个光滑的轻质挂钩,其下连着一个重为60N的物体.求两段细绳和水平方向的夹角和平衡时绳中的张力T.
如图所示,长为5m的细绳两端分别系于竖立在地面上相距为4m的两杆的顶端A、B.绳上挂一个光滑的轻质挂钩,其下连着一个重为60N的物体.求两段细绳和水平方向的夹角和平衡时绳中的张力T.分析:因为是一根绳子,故两端的拉力相等,由共点力的平衡条件可知两绳子的拉力的合力与物体的重力大小相等方向相反;作出平行四边形由几何关系可求得两绳与水平方向的夹角及张力.
解答:解:因为是一根绳,由绳子的特点可知两端绳子的张力大小相等;两端绳子与水平方向的夹角也相同,设为θ;
设总长度为L,两杆间的距离为S;若设挂钩左侧绳子长度是L1,则右侧绳子长度是(L-L1)
那么 L1×cosθ+(L-L1)×cosθ=S
即 L×cosθ=S
可知5cosθ=4;
故cosθ=0.8,即夹角为37°;sin37°=0.6;
物体悬挂处受两绳子的拉力及物体向下的拉力,由共点力的平衡条件可知,两拉力的合力与物体的重力等大反向;
由几何关系可知拉力F=
=
=50N.
故答案为:37°;50.
设总长度为L,两杆间的距离为S;若设挂钩左侧绳子长度是L1,则右侧绳子长度是(L-L1)
那么 L1×cosθ+(L-L1)×cosθ=S
即 L×cosθ=S
可知5cosθ=4;
故cosθ=0.8,即夹角为37°;sin37°=0.6;
物体悬挂处受两绳子的拉力及物体向下的拉力,由共点力的平衡条件可知,两拉力的合力与物体的重力等大反向;
由几何关系可知拉力F=
| G |
| 2sinθ |
| 60 |
| 2×0.6 |
故答案为:37°;50.

点评:本题的关键在于明确同一根绳子不论如何弯曲,只要是绷紧的则各部分拉力一定相等;故本题可以直接得出结论两边绳子与水平方向的夹角相等.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图所示,长为5m的细绳的两端分别系于竖立在地面上相距4m的两杆的顶端A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为12N的物体,平衡时,问:
如图所示,长为5m的细绳的两端分别系于竖立在地面上相距4m的两杆的顶端A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为12N的物体,平衡时,问: 如图所示,长为5m的细绳的两端分别系于竖立在水平地面上相距为4m的两根杆上的A、B两点(两点等高,距地面足够高),绳上挂有一个光滑的轻质挂钩,其下连着一个重为12N的物体平衡时,求
如图所示,长为5m的细绳的两端分别系于竖立在水平地面上相距为4m的两根杆上的A、B两点(两点等高,距地面足够高),绳上挂有一个光滑的轻质挂钩,其下连着一个重为12N的物体平衡时,求 如图所示,长为5m的细绳的两端分别系于竖立在地面上相距为4m的两杆的顶端A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为12N的物体,平衡时,绳中的张力T为多少??
如图所示,长为5m的细绳的两端分别系于竖立在地面上相距为4m的两杆的顶端A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为12N的物体,平衡时,绳中的张力T为多少?? 如图所示,长为5m的细绳的两端分别系于竖立在地面上相距为4m的两杆顶端A、B,绳上挂一个光滑的轻质挂钩,它钩着一个重为12N的物体.平衡时绳中张力为( )
如图所示,长为5m的细绳的两端分别系于竖立在地面上相距为4m的两杆顶端A、B,绳上挂一个光滑的轻质挂钩,它钩着一个重为12N的物体.平衡时绳中张力为( )