Question

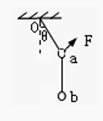（2009?扬州三模）如图，两个质量均为m的小球a，b用细线相连并悬挂于O点，用力F拉小球a，使整个装置处于平衡状态，且悬线O与竖直方向的夹角为θ=30°．则F的大小（　　）

• A．可能为

  3

  3

  mg
• B．可能为

  3

  2

  mg
• C．可能为mg
• D．不可能为

  2

  mg

Answer 1

分析：以两个小球组成的整体为研究对象，分析受力，作出力图，根据平衡条件，分析F可能的值．

解答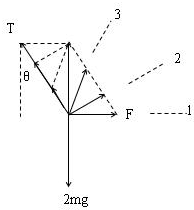：解：A、B、C以两个小球组成的整体为研究对象，分析受力，作出F在三个方向整体的受力图，可见，当F与绳子oa垂直时，F有最小值，即图中2位置，F的最小值为Fmin=2mgsinθ=mg．故AB错误，C正确．
D、当F竖直向上时，F=2mg；当F水平向右时，由平衡条件得F=2mgtanθ=

2 3

3

mg，则2mg＞F＞mg，而

2

mg在这个范围内，所以F可能为

2

mg．故D错误．
故选C

点评：本题是隐含的临界问题，运用图解法确定出F的范围，再进行选择．中等难度．