题目内容
如图所示,现有1 200个氢原子被激发到量子数为4的能级上,若这些受激氢原子最后都回到基态,则在此过程中发出的光子总数是多少( )
(假定处在量子数为n的激发态的氢原子跃迁到各较低能级的原子数都是处在该激发态能级上的原子总数的![]() )
)
A.2 200 B.2 000 C.1 200 , D.2 400
解析:由能级跃迁规律知:
处于量子数n=4的氢原子跃迁到n=3、n=2、n=1较低能级的原子数分别为1 200×![]() =400(个),则辐射光子数为400×3=1 200(个),而处于量子数n=3的400个氢原子向n=2,n=1跃迁,跃迁原子数分别为400×
=400(个),则辐射光子数为400×3=1 200(个),而处于量子数n=3的400个氢原子向n=2,n=1跃迁,跃迁原子数分别为400×![]() =200(个),则辐射光子数为200×2=400(个),而处于量子数n=2的原子总数为400+200=600(个),向基态跃迁则辐射光子数为600个.
=200(个),则辐射光子数为200×2=400(个),而处于量子数n=2的原子总数为400+200=600(个),向基态跃迁则辐射光子数为600个.
则此过程中发出光的总数为1 200+400+600=2 200(个).
答案:A

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
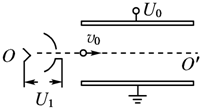 真空中的某装置如图所示,现有质子、氘核和α粒子都从O点由静止释放,经过相同加速电场和偏转电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点(已知质子、氘核和α粒子质量之比为1:2:4,电荷量之比为1:1:2,重力不计).下列说法中正确的是( )
真空中的某装置如图所示,现有质子、氘核和α粒子都从O点由静止释放,经过相同加速电场和偏转电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点(已知质子、氘核和α粒子质量之比为1:2:4,电荷量之比为1:1:2,重力不计).下列说法中正确的是( )| A、三种粒子在偏转电场中运动时间之比为2:1:1 | B、三种粒子出偏转电场时的速度相同 | C、在荧光屏上将只出现1个亮点 | D、偏转电场的电场力对三种粒子做功之比为1:1:2 |
 光电计时器是物理实验中经常用到的一种精密计时仪器,它由光电门和计时器两部分组成,光电门的一臂的内侧附有发光装置(发射激光的装置是激光二极管,发出的光束很细),如图实中的A和A′,另一臂的内侧附有接收激光的装置,如图实中的B和B′,当物体在它们之间通过时,二极管发出的激光被物体挡住,接收装置不能接收到激光信号,同时计时器就开始计时,直到挡光结束光电计时器停止计时,故此装置能精确地记录物体通过光电门所用的时间.现有一小球从两光电门的正上方开始自由下落,如图所示.
光电计时器是物理实验中经常用到的一种精密计时仪器,它由光电门和计时器两部分组成,光电门的一臂的内侧附有发光装置(发射激光的装置是激光二极管,发出的光束很细),如图实中的A和A′,另一臂的内侧附有接收激光的装置,如图实中的B和B′,当物体在它们之间通过时,二极管发出的激光被物体挡住,接收装置不能接收到激光信号,同时计时器就开始计时,直到挡光结束光电计时器停止计时,故此装置能精确地记录物体通过光电门所用的时间.现有一小球从两光电门的正上方开始自由下落,如图所示. (2011?石景山区一模)一轻质细绳一端系一质量为 m=0.05kg 的小球A,另一端套在光滑水平细轴O上,O到小球的距离为 L=0.1m,小球与水平地面接触,但无相互作用.在球的两侧等距离处分别固定一个光滑的斜面和一个挡板,二者之间的水平距离S=2m,如图所示.现有一滑块B,质量也为m,从斜面上高度h=3m处由静止滑下,与小球碰撞时没有机械能损失、二者互换速度,与档板碰撞时以同样大小的速率反弹.若不计空气阻力,并将滑块和小球都视为质点,滑块B与水平地面之间的动摩擦因数μ=0.25,g取 10m/s2.求:
(2011?石景山区一模)一轻质细绳一端系一质量为 m=0.05kg 的小球A,另一端套在光滑水平细轴O上,O到小球的距离为 L=0.1m,小球与水平地面接触,但无相互作用.在球的两侧等距离处分别固定一个光滑的斜面和一个挡板,二者之间的水平距离S=2m,如图所示.现有一滑块B,质量也为m,从斜面上高度h=3m处由静止滑下,与小球碰撞时没有机械能损失、二者互换速度,与档板碰撞时以同样大小的速率反弹.若不计空气阻力,并将滑块和小球都视为质点,滑块B与水平地面之间的动摩擦因数μ=0.25,g取 10m/s2.求: 如图所示,粗糙的斜面AB下端与光滑的圆弧轨道BCD相切于B,整个装置竖直放置,C是最低点,圆心角∠BOC=37°,圆弧轨道半径R=0.5m,斜面长L=2m,整个轨道除AB段以外都是光滑的,如图所示.现有一个质量m=0.1kg的小物块以初速度vo=4m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.60,cos37°=0.08).
如图所示,粗糙的斜面AB下端与光滑的圆弧轨道BCD相切于B,整个装置竖直放置,C是最低点,圆心角∠BOC=37°,圆弧轨道半径R=0.5m,斜面长L=2m,整个轨道除AB段以外都是光滑的,如图所示.现有一个质量m=0.1kg的小物块以初速度vo=4m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.60,cos37°=0.08).