题目内容
14.有一横截面积为S的铜导线,流经其中的电流强度为I,设每单位体积的导线内有n个自由电子,电子的电量为e,电子的定向移动速度为v,则一小段长为△l的铜导线内的电子个数为( )| A. | $\frac{IS△l}{ev}$ | B. | $\frac{I△l}{eS}$ | C. | $\frac{I△l}{e}$ | D. | $\frac{I△l}{ev}$ |
分析 根据电流的微观表达式I=nevs,求出在△t时间内通过导体横截面的自由电子的电量,每个电子的电量为e,再确定通过导体横截面的自由电子的数目.
解答 解:根据电流的微观表达式I=nevs,设长为△l的铜导线内的电子在△t时间内通过某一个导体横截面,则电量q=I△t,
则$△t=\frac{△l}{v}$
在△t时间内,通过导体横截面的自由电子的数目为N=$\frac{q}{e}$,
将I=nevs代入得N=$\frac{nevs△t}{e}$=n△ls.
若考虑:$ns=\frac{I}{ev}$,则:N=$\frac{I△l}{ev}$.故D正确,ABC错误.
故选:D.
点评 本题考查电流的微观表达式和定义式综合应用的能力,电流的微观表达式I=nqvs,是联系宏观与微观的桥梁,常常用到.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
2. 如图所示,在真空中A、B两点分别放置等量异号电荷,在电场中,通过A、B两点的竖直平面内,以AB中线为对称轴取一个矩形路径abcd,e、f、g、h分别为ad、bc、ab和AB的中点.现将一电子在电场中沿下列直线运动时,则以下判断正确的是( )
如图所示,在真空中A、B两点分别放置等量异号电荷,在电场中,通过A、B两点的竖直平面内,以AB中线为对称轴取一个矩形路径abcd,e、f、g、h分别为ad、bc、ab和AB的中点.现将一电子在电场中沿下列直线运动时,则以下判断正确的是( )
 如图所示,在真空中A、B两点分别放置等量异号电荷,在电场中,通过A、B两点的竖直平面内,以AB中线为对称轴取一个矩形路径abcd,e、f、g、h分别为ad、bc、ab和AB的中点.现将一电子在电场中沿下列直线运动时,则以下判断正确的是( )
如图所示,在真空中A、B两点分别放置等量异号电荷,在电场中,通过A、B两点的竖直平面内,以AB中线为对称轴取一个矩形路径abcd,e、f、g、h分别为ad、bc、ab和AB的中点.现将一电子在电场中沿下列直线运动时,则以下判断正确的是( )| A. | 由g→h→f的过程中,电子所受的电场力方向不变 | |
| B. | 由g→h→f的过程中,电子所受的电场力一直增大 | |
| C. | 由g→h的过程中,电势降低,电子的电势能增大 | |
| D. | 由d→e→a的过程中,电子d的电势能先减小后增大,电势能的总增量为零 |
19. 如图所示,在竖直方向上,A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上,B、C两物体通过细线绕过轻质定滑轮相连,C放在倾角α=30°的固定光滑斜面上,用手拿住C,使细线刚刚拉直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态,释放C后沿斜面下滑,A刚要离开地面时,B获得最大速度,则下列说法正确的是( )
如图所示,在竖直方向上,A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上,B、C两物体通过细线绕过轻质定滑轮相连,C放在倾角α=30°的固定光滑斜面上,用手拿住C,使细线刚刚拉直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态,释放C后沿斜面下滑,A刚要离开地面时,B获得最大速度,则下列说法正确的是( )
 如图所示,在竖直方向上,A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上,B、C两物体通过细线绕过轻质定滑轮相连,C放在倾角α=30°的固定光滑斜面上,用手拿住C,使细线刚刚拉直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态,释放C后沿斜面下滑,A刚要离开地面时,B获得最大速度,则下列说法正确的是( )
如图所示,在竖直方向上,A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上,B、C两物体通过细线绕过轻质定滑轮相连,C放在倾角α=30°的固定光滑斜面上,用手拿住C,使细线刚刚拉直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态,释放C后沿斜面下滑,A刚要离开地面时,B获得最大速度,则下列说法正确的是( )| A. | 从释放C到物体A刚要离开地面时,物体C沿斜面下滑的距离为$\frac{4mg}{k}$ | |
| B. | 物体C的质量M=4m | |
| C. | 从释放C到A刚要离开地面的过程中,细线的拉力大小先变小后变大 | |
| D. | 从释放C到A刚要离开地面的过程中,物体C的重力势能的减少量大于其动能的增加量 |
6.关于电流强度的下列说法中,正确的是( )
| A. | 导体中的电流强度越大,表示通过其横截面的电量越多 | |
| B. | 在相同时间内,通过导体横截面的电量越多,导体中电流强度就越小 | |
| C. | 通电时间越短,电流强度越大 | |
| D. | 单位时间内通过导体横截面的电量越多,导体中电流强度越大 |
3.关于弹力,下列说法中正确的是( )
| A. | 两物体相互接触就一定产生弹力 | |
| B. | 轻绳所受弹力方向一定沿绳,直杆所受弹力方向不一定沿直杆 | |
| C. | 放在桌面上静止的重物对地面有压力 | |
| D. | 只有发生弹性形变的物体才会对与它接触的物体产生弹力作用 |
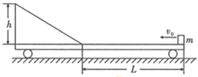 如图所示,光滑水平面上有一平板车,车的上表面在一段长L=1.5m的粗糙水平轨道,水平轨道左侧是一高h=0.25m的三角形木块,现将一质量m=1.0kg的小物块(可视为质点)从平板车的右端以水平向左的初速度v0滑上平板车,车和三角形木块的总质量M=4.0kg的,小物块与水平轨道间的动摩擦因数μ=0.5,三角形木块表面光滑,小物块冲上木块时,无能量损失,取g=10m/s2,则要使小物块能够滑到斜面的顶端,v0至少为多大?
如图所示,光滑水平面上有一平板车,车的上表面在一段长L=1.5m的粗糙水平轨道,水平轨道左侧是一高h=0.25m的三角形木块,现将一质量m=1.0kg的小物块(可视为质点)从平板车的右端以水平向左的初速度v0滑上平板车,车和三角形木块的总质量M=4.0kg的,小物块与水平轨道间的动摩擦因数μ=0.5,三角形木块表面光滑,小物块冲上木块时,无能量损失,取g=10m/s2,则要使小物块能够滑到斜面的顶端,v0至少为多大?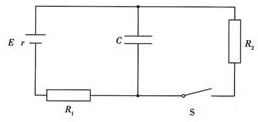 如图所示的电路,其中电源的电动势E=12V,内阻r=2Ω,电阻R1=6Ω,R2=4Ω,电容器的电容C=2μF.开关S是闭合的,现将开关S断开,求:
如图所示的电路,其中电源的电动势E=12V,内阻r=2Ω,电阻R1=6Ω,R2=4Ω,电容器的电容C=2μF.开关S是闭合的,现将开关S断开,求: 广东省第十四届运动会于2015年8月在湛江举行.田径100米决赛是竞争最为激烈的比赛项目之一.某运动员在100m训练中成绩刚好为10.00s.
广东省第十四届运动会于2015年8月在湛江举行.田径100米决赛是竞争最为激烈的比赛项目之一.某运动员在100m训练中成绩刚好为10.00s.