题目内容
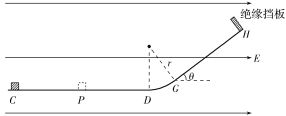
【题目】如图，轨道CDGH位于竖直平面内，其中圆弧段DG与水平段CD及倾斜段GH分别相切于D点和G点，圆弧段和倾斜段均光滑，在H处固定一垂直于轨道的绝缘挡板，整个轨道绝缘且处于水平向右的匀强电场中。一带电物块由C处静止释放，经挡板碰撞后(碰撞后速度大小不变)滑回CD段中点P处时速度恰好为零。已知物块的质量m＝4×10－3 kg，所带的电荷量q＝＋3×10－6 C；电场强度E＝1×104 N/C；CD段的长度L＝0.8 m，圆弧DG的半径r＝0.2 m，GH段与水平面的夹角为θ，且sin θ＝0.6，cos θ＝0.8；不计物块与挡板碰撞时的动能损失，物块可视为质点，重力加速度g取10 m/s2。
(1)求物块与轨道CD段的动摩擦因数μ；
(2)求物块第一次碰撞挡板时的动能Ek；
(3)物块在水平轨道上运动的总路程；
(4)物块碰撞挡板时的最小动能。
【答案】(1)0.25 (2)0.018 J (3)2.4 m (4)0.002 J
【解析】(1)物块由C处释放后经挡板碰撞滑回P点过程中，由动能定理得
qE·
－μmg(L＋)＝0①(2分)
由①式代入数据得μ＝
＝0.25②
(2)物块在GH段运动时，由于qEcos θ＝mgsin θ，所以做匀速直线运动③
由C运动至H过程中，由动能定理得
qEL－μmgL＋qErsin θ－mgr(1－cos θ)＝Ek－0④
由③式代入数据得Ek＝0.018 J⑤
(3)物块最终会在DGH间来回往复运动，物块在D点的速度为0
设物块能在水平轨道上运动的总路程为s，由能量转化与守恒定律可得qEL＝μmgs⑥
由②③⑥式代入数据得s＝2.4 m⑦
(4)物块碰撞挡板的最小动能E0等于往复运动时经过G点的动能，由动能定理得
qErsin θ－mgr(1－cos θ)＝E0－0⑧
由③⑧式代入数据得E0＝0.002 J⑨
