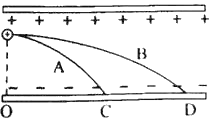
题目内容
【题目】设均匀球体在空气中下落时,空气对球体的阻力的大小只与球的最大截面积成正比。某同学用轻质细绳![]() 连接球A与球B,再用轻质细绳
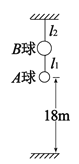
连接球A与球B,再用轻质细绳![]() 将球B悬挂于上方某位置点,当两球处于平衡状态时,球A与水平地面的距离为18m,此时两细绳拉力的大小分别是2N、3N。已知球A与球B的半径之比为1:2,当地重力加速度为10m/s2。第一次,若只剪断细绳
将球B悬挂于上方某位置点,当两球处于平衡状态时,球A与水平地面的距离为18m,此时两细绳拉力的大小分别是2N、3N。已知球A与球B的半径之比为1:2,当地重力加速度为10m/s2。第一次,若只剪断细绳![]() ,A球经2s落地。第二次,若只剪断细绳
,A球经2s落地。第二次,若只剪断细绳![]() ,A球经多长时间落地?(结果保留两位有效数字)
,A球经多长时间落地?(结果保留两位有效数字)
【答案】2.3s
【解析】试题分析:设球A与球B的质量分别为mA、mB, 分别对球A和整体受力分析,求出质量和阻力,第二次剪断细线l2后,球A与球B一起加速下落,对球整体受力分析根据牛顿第二定律,求出加速度,再根据运动学公式求出时间。
设球A与球B的质量分别为mA、mB。对球A受力分析得:T1 = mAg
静止时对整体受力分析得:T2 = mAg+mBg,
第一次剪断细线l1后,球A加速下落,根据运动学公式得:h = a1tA2
对球A受力分析得:mAg - fA = mAa1
代入数据求得:mA = 0.2kg、mB = 0.1kg、a1 = 9m/s2、fA = 0.2N,
根据题意: ![]() ,解得:f2 = 0.8N
,解得:f2 = 0.8N
第二次剪断细线l2后,球A与球B一起加速下落,
对球整体受力分析得:mAg+mBg - fA - fB =(mA+mB)a2
根据运动学公式得: ![]()
代入数据求得: ![]()

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目