题目内容
19. 如图所示是一边长为10cm的实心立方体木块,一只昆虫从A点爬到G点,下列说法正确的是( )
如图所示是一边长为10cm的实心立方体木块,一只昆虫从A点爬到G点,下列说法正确的是( )| A. | 该昆虫的路程有若干种可能性,其中最短路程为(10+10$\sqrt{2}$)cm | |
| B. | 该昆虫的位移大小为10$\sqrt{5}$cm | |
| C. | 该昆虫的路程有若干种可能性,其中最短路程为10$\sqrt{5}$cm | |
| D. | 该昆虫的位移大小为10$\sqrt{3}$cm |
分析 位移是初位置指向末位置的有向线段,从相邻的两个面到达G才可能最短,我们可以把面AEFD和面CDFG展开,根据几何关系求解.
解答 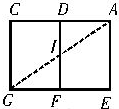 解:AC、其最短路程分析可知:应该从相邻的两个面到达G才可能最短,我们可以把面AEFD和面CDFG展开,如图,
解:AC、其最短路程分析可知:应该从相邻的两个面到达G才可能最短,我们可以把面AEFD和面CDFG展开,如图,
连接A与G,AIG的长度就是最短路程s=$\sqrt{1{0}^{2}+{20}^{2}}$=10$\sqrt{5}$cm,故A错误,C正确;
BD、昆虫只能沿木块表面从A点到G点,其运动轨迹可以有各种不同的情况,但是,其起点和终点是相同的,即位移相同,为立方体对角线的长度x=$\sqrt{1{0}^{2}+(10\sqrt{2})^{2}}$=10$\sqrt{3}$cm,故B错误,D正确;
故选:CD
点评 本题主要考查了路程和位移的区别与联系,知道位移是初位置指向末位置的有向线段,路程是运动轨迹的长度.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
9. 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示.下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示.下列说法中正确的是( )
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示.下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示.下列说法中正确的是( )| A. | 图线1表示竖直分运动的v-t图线 | B. | 图线2表示水平分运动的v-t图线 | ||
| C. | 图线1表示水平分运动的v-t图线 | D. | 以上说法都不对 |
7.下列描述的匀变速直线运动中,可能存在的是( )
| A. | 速度变化很大,加速度却很小 | |
| B. | 速度变化的方向为正,加速度方向为负 | |
| C. | 速度方向为正,加速度方向为负 | |
| D. | 速度越来越大,加速度越来越小 |

 如图所示,长为2.0m,高为0.8m,质量为12kg且上表面光滑的木箱,以一定的初速度冲上一与木箱间的动摩擦因数为0.3的水平面,当木箱的速度减少到7.0m/s时,把一质量为1.0kg的小球轻轻放在长木箱的前端,若重力加速度g取10m/s2,求小球落地时,小球距木箱末端的水平距离.
如图所示,长为2.0m,高为0.8m,质量为12kg且上表面光滑的木箱,以一定的初速度冲上一与木箱间的动摩擦因数为0.3的水平面,当木箱的速度减少到7.0m/s时,把一质量为1.0kg的小球轻轻放在长木箱的前端,若重力加速度g取10m/s2,求小球落地时,小球距木箱末端的水平距离.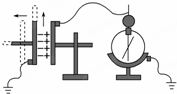 用如图所示装置可以研究影响平等板电容器电容的因素,设两极板正对面积为S,两极板间的距离为d,板间电介质的介电常数为?,静电计指针偏角为θ,实验中,极板所带电荷量不变,
用如图所示装置可以研究影响平等板电容器电容的因素,设两极板正对面积为S,两极板间的距离为d,板间电介质的介电常数为?,静电计指针偏角为θ,实验中,极板所带电荷量不变,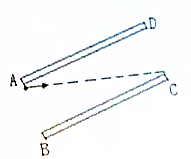 如图所示,平行板电容器的两个极板AD与BC的长度为4cm,它们相距3cm,上极板的A端与下极板的C端在同一水平面上,两极板与一直流电源相连,若一质量为4×10-3kg、带电量为-3×10-7C的带电微粒从A点进入电容器间电场后恰能沿图中所示的AC连线做直线运动,且刚好能够到达C点(重力加速度取10m/s2)试求:
如图所示,平行板电容器的两个极板AD与BC的长度为4cm,它们相距3cm,上极板的A端与下极板的C端在同一水平面上,两极板与一直流电源相连,若一质量为4×10-3kg、带电量为-3×10-7C的带电微粒从A点进入电容器间电场后恰能沿图中所示的AC连线做直线运动,且刚好能够到达C点(重力加速度取10m/s2)试求:
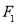 的力压弹簧的另一端,平衡时长度为
的力压弹簧的另一端,平衡时长度为 ;改用大小为
;改用大小为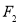 的力拉弹簧,平衡时长度为
的力拉弹簧,平衡时长度为 .弹簧的拉伸或压缩均在弹性限度内,则该弹簧的劲度系数是 .
.弹簧的拉伸或压缩均在弹性限度内,则该弹簧的劲度系数是 .