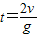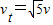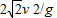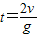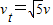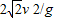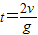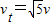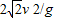题目内容
平抛物体的初速度为v0,当水平方向分位移与竖直方向分位移相等时( )
分析:通过竖直分位移与水平分位移大小相等,求出时间,根据时间可求出竖直方向的分速度以及速度的大小和方向.
解答:解:A、竖直分位移与水平分位移大小相等,有v0t=
gt2,所以运动的时间t=
.故A正确.
B、平抛运动瞬时速度的大小为v=
=
=
v0.故B正确.
C、竖直方向上的分速度vy=gt=2v0,与水平分速度不等.故C错误.
D、水平位移x=v0t=
,所以物体的位移s=
s=
.故D正确.
故选ABD.
| 1 |
| 2 |
| 2v0 |
| g |
B、平抛运动瞬时速度的大小为v=
| vx2+vy2 |
| v02+(2v0)2 |
| 5 |
C、竖直方向上的分速度vy=gt=2v0,与水平分速度不等.故C错误.
D、水平位移x=v0t=
| 2v02 |
| g |
| 2 |
2
| ||
| g |
故选ABD.
点评:解决本题的关键掌握处理平抛运动的方法,平抛运动可分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动.且分运动与合运动具有等时性.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
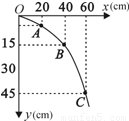 在“研究平抛物体的运动”的实验中,记录了下图所示的一段轨迹ABC.已知物体是由原点O水平抛出的,C点的坐标为(60,45),则平抛物体的初速度为v=______m/s,物体经过B点时的速度vB的大小为vB=______
在“研究平抛物体的运动”的实验中,记录了下图所示的一段轨迹ABC.已知物体是由原点O水平抛出的,C点的坐标为(60,45),则平抛物体的初速度为v=______m/s,物体经过B点时的速度vB的大小为vB=______